Theo giả thiết ta có:

\(\begin{array}{l}2\left(x^{2}+y^{2}+2\right)+\log _{2}\left(\frac{2}{x}+\frac{2}{y}\right)=\frac{1}{2}(x y-4)^{2} \\\Leftrightarrow 2(x+y)^{2}-4 x y+8+\log _{2}\left[\frac{2(x+y)}{x y}\right]=\frac{1}{2}(x y)^{2}-4 x y+8 \\\Leftrightarrow 2(x+y)^{2}+\log _{2}(x+y)=2\left(\frac{x y}{2}\right)^{2}+\log _{2}\left(\frac{x y}{2}\right) \quad(*) .\end{array}\)

Xét hàm số \(f(t)=2 t^{2}+\log _{2} t\), với \(t\gt 0\).

Có \(f^{\prime}(t)=4 t+\frac{1}{t \cdot \ln 2}\gt 0, \forall t>0\). Suy ra hàm số \(f(t)\) đồng biến trên khoảng \((0 ;+\infty)\).

Do đó ta có \(\left({ }^{*}\right) \Leftrightarrow f(x+y)=f\left(\frac{x y}{2}\right) \Leftrightarrow x+y=\frac{x y}{2} \Leftrightarrow x(y-2)=2 y\).

Mà theo giả thiết \(x, y>0\) nên suy ra \(y>2\) (tương tự \(x>2\) ) và \(x=\frac{2 y}{y-2}\).

Đặt \(P=x+4 y \Rightarrow P=\frac{2 y}{y-2}+4 y=\left[4(y-2)+\frac{4}{y-2}\right]+10\).

Theo bđt AM-GM ta có \(P \geq 2 \sqrt{16}+10=18\). Dấu bằng xảy ra khi

\(\left\{\begin{array} { l } { y = 3 } \\{ x = \frac { 2 y } { y - 2 } }\end{array} \Leftrightarrow \left\{\begin{array}{l}y=3 \\x=6\end{array} \Rightarrow \frac{x}{y}=2\right.\right. \text {. }\)

Cách 2 tìm minP:

Xét hàm số \(g(y)=\frac{2 y}{y-2}+4 y\), với \(y\gt 2\).

Có \(g^{\prime}(y)=4-\frac{4}{(y-2)^{2}}, g^{\prime}(y)=0 \Leftrightarrow(y-2)^{2}=1 \Leftrightarrow\left[\begin{array}{l}y=1(L) \\ y=3(t / m)\end{array}\right.\).

Ta có bảng biến thiên

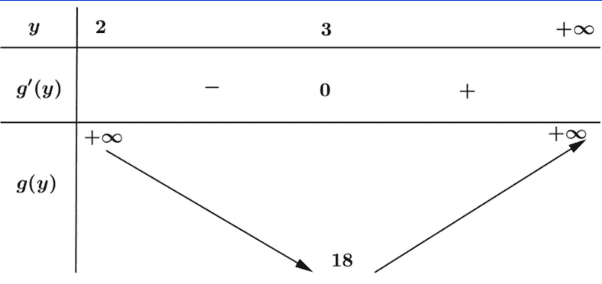
Từ bảng biến thiên suy ra min \(P=18\), đạt được khi \(\left\{\begin{array}{l}y=3 \\ x=\frac{2 y}{y-2}\end{array} \Leftrightarrow\left\{\begin{array}{l}y=3 \\ x=6\end{array} \Rightarrow \frac{x}{y}=2\right.\right.\).