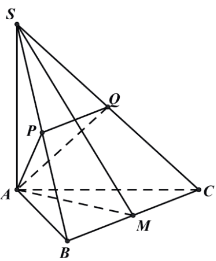
Sai: Gọi \(M\) là trung điểm của cạnh \(B C\).

Ta có: \(B C \perp A M\) ( \(A M\) là đường trung tuyến của \(\triangle A B C\) đều) và \(B C \perp S A(S A \perp(A B C))\)

Do đó: \(B C \perp(S A M) \Rightarrow B C \perp S M\)

Ta có: \(\left\{\begin{array}{l}(S B C) \cap(A B C)=B C \\ S M \perp B C, S M \subset(S B C) \\ A M \perp B C, A M \subset(A B C)\end{array}\right.\)

Do đó: góc tạo bởi mặt phẳng \((S B C)\) và mặt phẳng \((A B C)\) là góc \(S M A\)

Xét tam giác đều \(A B C: A M=\frac{a \sqrt{3}}{2}\)

Xét tam giác vuông \(S M A\) có: \(\tan S M A=\frac{S A}{A M}=\frac{\frac{a}{2}}{\frac{a \sqrt{3}}{2}}=\frac{\sqrt{3}}{3}\) suy ra: \(S M A=30^{\circ}\)

Vậy góc tạo bởi mặt phẳng \((S B C)\) và mặt phẳng \((A B C)\) bằng \(30^{\circ}\).