Cho hình chóp \(S . A B C D\) đáy \(A B C D\) là hình thoi, \(S A=S C\). Khẳng định nào sau đây đúng?
A.
\((S B D) \perp(A B C D)\).
B.
\((S B C) \perp(A B C D)\).
C.
\((S A D) \perp(A B C D)\)
D.
\((S B A) \perp(A B C D)\)
Giải thích:
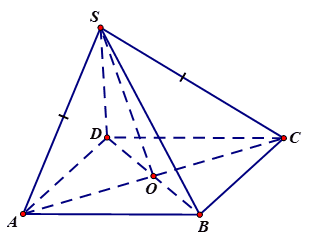
Ta có: \(\mathrm{AC} \perp \mathrm{BD}\) (1) (giả thiết)
\(\mathrm{AC} \perp \mathrm{SO}\) (2) ( \(\mathrm{Do} \triangle \mathrm{SAC}\) là tam giác cân tại A và O là trung điểm của AC nên SO là đường cao của tam giác)
Từ (1) và (2) suy ra: \(\mathrm{AC} \perp(\mathrm{SBD})\) mà \(\mathrm{AC} \subset(\mathrm{ABCD})\) nên \((\mathrm{SBD}) \perp(\mathrm{ABCD})\)
Câu hỏi này nằm trong: