Cho hình lăng trụ đứng \(A B C \cdot A^{\prime} B^{\prime} C^{\prime}\) có đáy \(A B C\) là tam giác vuông tại \(B, A B=B C=a\), \(B B^{\prime}=a \sqrt{3}\). Tính góc giữa đường thẳng \(A^{\prime} B\) và mặt phẳng \(\left(B C C^{\prime} B^{\prime}\right)\).
A.
\(45^{\circ}\).
B.
\(30^{\circ}\).
C.
\(60^{\circ}\).
D.
\(90^{\circ}\).
Giải thích:
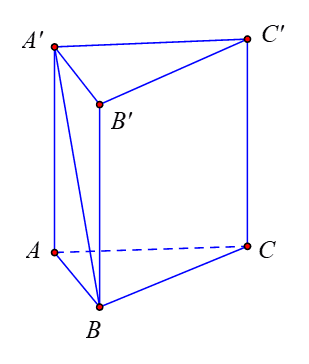
Hình lăng trụ đứng \(A B C . A^{\prime} B^{\prime} C^{\prime}\) nên \(B B^{\prime} \perp\left(A^{\prime} B^{\prime} C^{\prime}\right) \Rightarrow B B^{\prime} \perp A^{\prime} B^{\prime} \Rightarrow A^{\prime} B^{\prime} \perp B B^{\prime}\)
Bài ra có \(A B \perp B C \Rightarrow A^{\prime} B^{\prime} \perp B^{\prime} C^{\prime}\).
Kết hợp với \((1) \Rightarrow A^{\prime} B^{\prime} \perp\left(B C C^{\prime} B^{\prime}\right) \Rightarrow \widehat{\left(A^{\prime} B ;\left(B C C^{\prime} B^{\prime}\right)\right)}=\widehat{A^{\prime} B B^{\prime}}\)
\(\Rightarrow \tan \left(\widehat{\left.A^{\prime} B ;\left(B C C^{\prime} B^{\prime}\right)\right)}=\tan \widehat{A^{\prime} B B^{\prime}}=\frac{A^{\prime} B^{\prime}}{B B^{\prime}}=\frac{a}{a \sqrt{3}}=\frac{1}{\sqrt{3}} \Rightarrow \overline{\left(A^{\prime} B ;\left(B C C^{\prime} B^{\prime}\right)\right)}=30^{\circ} .\right.\)Câu hỏi này nằm trong: