Cho khối chóp \(S \cdot A B C D\) có đáy là hình bình hành. Gọi \(M, N\) là hai điểm nằm trên hai cạnh \(S C, S D\) sao cho \(\frac{S M}{S C}=\frac{1}{2}, \frac{S N}{N D}=2\), biết \(G\) là trọng tâm tam giác \(S A B\). Tỉ số thể tích \(\frac{V_{G . M N D}}{V_{S . A B C D}}=\frac{a}{b}\) với \(\frac{a}{b}\) là phân số tối giản và \(a, b \in \mathbb{Z}\). Tính \(a+b\).
Giải thích:
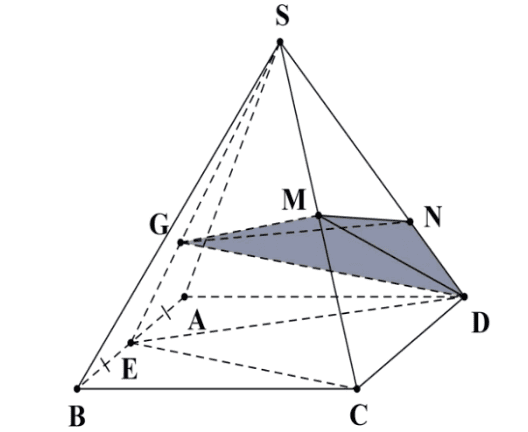
Gọi \(E\) là trung điểm cạnh \(A B ; \frac{S N}{N D}=\frac{1}{2} \Rightarrow \frac{S N}{S D}=\frac{2}{3}\).
Ta có: \(S_{\triangle E C D}=\frac{1}{2} S_{A B C D}\) nên \(V_{S . E C D}=\frac{1}{2} V_{S . A B C D}\).
Lại có: \(V_{D . M N G}=\frac{N D}{S N} V_{S . M N G}=\frac{1}{2} V_{S . M N G}\)
Khi đó: \(V_{S . M N G}=\frac{S G}{S E} \cdot \frac{S M}{S C} \cdot \frac{S N}{S D} \cdot V_{S . C D E}=\frac{2}{3} \cdot \frac{1}{2} \cdot \frac{2}{3} \cdot \frac{1}{2} V_{S . A B C D}=\frac{1}{9} V_{S . A B C D}\) nên \(V_{D . M N G}=\frac{1}{18} V_{S . A B C D}\).
Do vậy \(\frac{V_{G . M N D}}{V_{S . A B C D}}=\frac{1}{18} \Rightarrow\left\{\begin{array}{l}a=1 \\ b=18\end{array} \Rightarrow a+b=19\right.\).
Câu hỏi này nằm trong: