Trong mặt phẳng tọa độ \(O x y\), cho hình thoi \(A B C D\) có \(A C=2 B D\) và đường tròn tiếp xúc với các cạnh của hình thoi có phương trình \((C): x^{2}+y^{2}=4\). Viết phương trình chính tắc của elip \((E)\) đi qua các đỉnh \(A, B, C, D\) của hình thoi với điểm \(A\) nằm trên trục \(O x\).
Giải thích:
Giả sử phương trình elip \((E)\) là \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1(a\gt b>0)\).
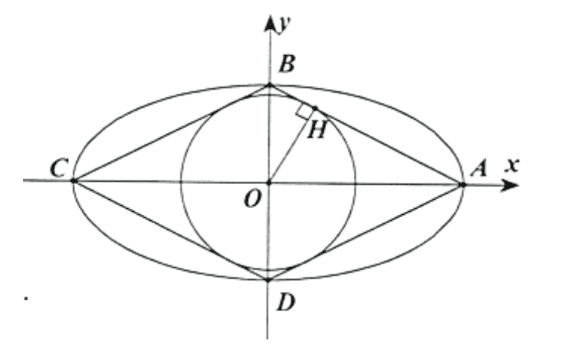
Đường tròn \((C): x^{2}+y^{2}=4\) có tâm \(O(0 ; 0)\) và bán kính \(R=2\).
Vì \((C)\) tiếp xúc với các cạnh của hình thoi và \(A \in O x\) nên \(C \in O x\) và \(B, D \in O y\).
Các điểm \(A, B, C, D \in(E)\) nên \(A, B, C, D\) là các đỉnh của \((E)\).
\(A, B \in(E) \Rightarrow A(a ; 0), B(0 ; b) \Rightarrow O A=a, O B=b \text {. }\)Vì \(O A=2 O B\) nên \(a=2 b\).
Kẻ \(O H \perp A B(H \in A B)\).Ta có \(O H=R=2\).
Tam giác \(A B O\) vuông tại \(O\) có
\(\frac{1}{O H^{2}}=\frac{1}{O A^{2}}+\frac{1}{O B^{2}} \Leftrightarrow \frac{1}{4}=\frac{1}{a^{2}}+\frac{4}{a^{2}} \Leftrightarrow a^{2}=20 \Rightarrow b^{2}=5 .\)Vậy phương trình \((E)\) là \(\frac{x^{2}}{20}+\frac{y^{2}}{5}=1\).
Câu hỏi này nằm trong: