Cho lăng trụ đứng \(A B C . A^{\prime} B^{\prime} C^{\prime}\) có \(A C=a, B C=2 a, A C B=120^{\circ}\). Gọi \(M\) là trung điểm của \(B B^{\prime}\) Khi đó:
a) \(d\left(C C^{\prime},\left(A B B^{\prime} A^{\prime}\right)\right)=\frac{a \sqrt{21}}{7}\)
A.
B.
Giải thích:
Ta có: \(C C^{\prime} / / B B^{\prime} \Rightarrow C C^{\prime} / /\left(A B B^{\prime} A^{\prime}\right)\) nên \(d\left(C C^{\prime},\left(A B B^{\prime} A^{\prime}\right)\right)=d\left(C,\left(A B B^{\prime} A^{\prime}\right)\right)\).
Trong mặt phẳng \((A B C)\) kẻ \(C H \perp A B\) tại \(H~~~~(1)\)
Vì \(A B C . A^{\prime} B^{\prime} C^{\prime}\) là hình lăng trụ đứng nên \(A A^{\prime} \perp(A B C) \Rightarrow C H \perp A A^{\prime}~~~~(2)\)
Từ (1) và (2) suy ra \(C H \perp\left(A B B^{\prime} A^{\prime}\right) \Rightarrow d\left(C,\left(A B B^{\prime} A^{\prime}\right)\right)=C H\).
Xét tam giác \(A B C\) có \(A B^{2}=C A^{2}+C B^{2}-2 C A.C B . \cos 120^{\circ}=7 a^{2} \Rightarrow A B=a \sqrt{7}\).
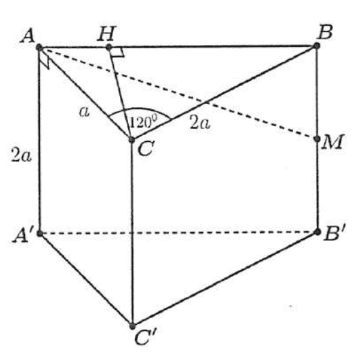
Diện tích tam giác \(A B C\) là: \(S_{\triangle A B C}=\frac{1}{2} C A . C B. \sin C=\frac{1}{2} A B.C H\)
\[\Rightarrow C H=\frac{C A . C B. \sin 120^{\circ}}{A B}=\frac{a . 2 a . \frac{\sqrt{3}}{2}}{a \sqrt{7}}=\frac{a \sqrt{2}}{7}\]Vậy \(d\left(C C^{\prime},\left(A B B^{\prime} A^{\prime}\right)\right)=C H=\frac{a \sqrt{2}}{7}\).
Câu hỏi này nằm trong: