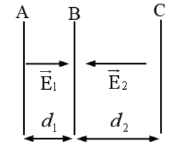
Cho ba bản kim loại phẳng \(\mathrm{A}, \mathrm{B}, \mathrm{C}\) đặt song song như hình vẽ. \(\mathrm{d}_{1}=5 \mathrm{~cm}\), \(\mathrm{d}_{2}=8 \mathrm{~cm}\). Các bản được tích điện và điện trường giữa các bản là đều, có chiều như hình vẽ với độ lớn: \(\mathrm{E}_{1}=4.10^{4} \mathrm{~V} / \mathrm{m}, \mathrm{E}_{2}=5.10^{4} \mathrm{~V} / \mathrm{m}\). Chọn gốc điện thế tại bản A , tìm điện thế \(\mathrm{V}_{\mathrm{C}}\).
A.
2600V
B.
2000V
C.
3200V
D.
3500V
Giải thích:
- Vì \(\overrightarrow{\mathrm{E}_{1}}\) hướng từ A đến B , ta có: \(U_{A B}=V_{A}-V_{B}=E_{1} \cdot d_{1}\)
Gốc điện thế tại bản \(\mathrm{A}: V_{A}=0\)
Suy ra: \(V_{B}=V_{A}-E_{1} d_{1}=0-4 \cdot 10^{4} \cdot 5 \cdot 10^{-2}=-2000 \mathrm{~V}\)
- Vì \(\overrightarrow{\mathrm{E}_{2}}\) hướng từ C đến B , ta có: \(U_{C B}=V_{C}-V_{B}=E_{2} \cdot d_{2}\)
Suy ra: \(V_{C}=V_{B}+E_{2} d_{2}=-2000+5 \cdot 10^{4} \cdot 8 \cdot 10^{-2}=2000 \mathrm{~V}\)
Câu hỏi này nằm trong: