Vì \((S A B),(S A D)\) cùng vuông góc với mặt phẳng \((A B C D)\) mà \((S A B) \cap(S A D)=S A\).

Suy ra \(S A \perp(A B C D)\).

Ta có \(V_{S . A B C D}=\frac{1}{3} A B^{2} .S A=\frac{1}{3} a^{2} .S A=\frac{a^{3}}{3} \Rightarrow S A=a\).

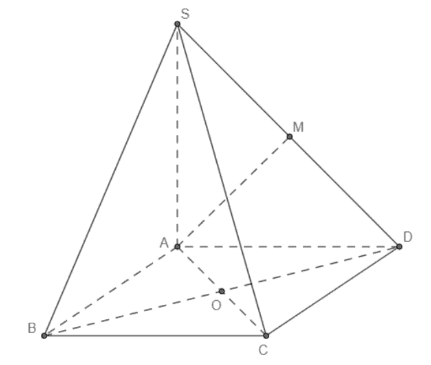
Gọi \(H\) là hình chiếu vuông góc của \(B\) lên mặt phẳng \((S C D)\).

Có \(S B \cap(S C D)=S\)

\(\Rightarrow S H\) là hình chiếu của \(S B\) lên mặt phẳng \((S C D) \Rightarrow(S B,(S C D))=(S B, S H)=B S H=\varphi\).

Ta có: \(\sin \varphi=\frac{B H}{S B}=\frac{d(B,(S C D))}{S B}=\frac{d(A,(S C D))}{S B}=\frac{S A \times A D}{S D \times S B}=\frac{a \times a}{a \sqrt{2} \times a \sqrt{2}}=\frac{1}{2} \Rightarrow \varphi=30^{\circ}\).

Vậy góc \(\varphi\) giữa đường thẳng \(S B\) và mặt phẳng \((S C D)\) bằng \(\varphi=30^{\circ}\).