Cho hình lăng trụ tam giác đều \(A B C . A^{\prime} B^{\prime} C^{\prime}\) có các cạnh đều bằng \(a\). Tính diện tích \(S\) của mặt cầu đi qua 6 đỉnh của hình lăng trụu đó.
A.
\(S=\frac{7 \pi a^{2}}{3}\)
B.
\(S=\frac{7 a^{2}}{3}\)
C.
\(S=\frac{49 \pi a^{2}}{144}\)
D.
\(S=\frac{49 a^{2}}{114}\)
Giải thích:
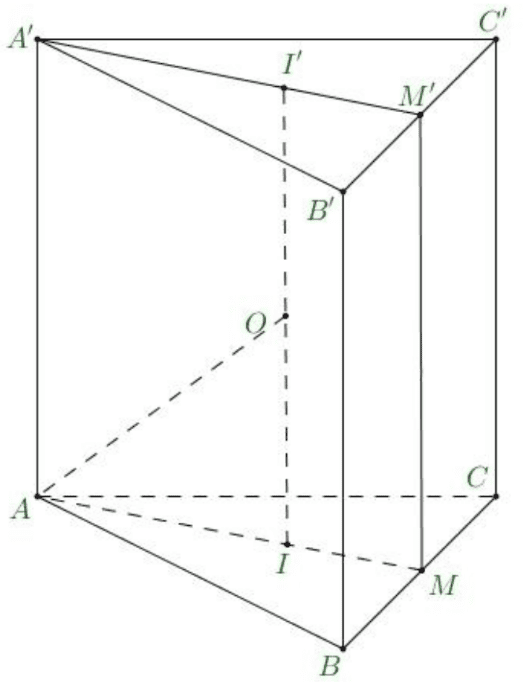
Gọi \(I, I^{\prime}\) lần lượt là trọng tâm tam giác \(A B C, A^{\prime} B^{\prime} C^{\prime}, O\) là trung điểm của \(I I^{\prime}\).
Khi đó \(O\) là tâm mặt cầu ngoại tiếp hình lăng trụ.
Ta có \(A I=\frac{2}{3} A M=\frac{a \sqrt{3}}{3}, O I=\frac{a}{2}\).
Bán kính mặt cầu ngoại tiếp hình lăng trụ \(R=O A=\sqrt{O I^{2}+A I^{2}}=\sqrt{\left(\frac{a}{2}\right)^{2}+\left(\frac{a}{\sqrt{3}}\right)^{2}}=\frac{a \sqrt{7}}{\sqrt{12}}\).
Diện tích mặt cầu \(S=4 \pi R^{2}=4 \pi \cdot \frac{7 a^{2}}{12}=\frac{7 \pi a^{2}}{3}\).
Câu hỏi này nằm trong: