Cho hình lăng trụ \(A B C \cdot A^{\prime} B^{\prime} C^{\prime}\) có đáy \(A B C\) là tam giác vuông tại \(C\). Tính góc \(\left(A C ; B^{\prime} C^{\prime}\right)\).
Giải thích:
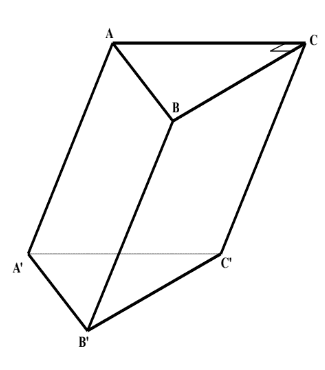
Vì \(B^{\prime} C^{\prime} / / B C\) nên \(\left(A C, B^{\prime} C^{\prime}\right)=(A C, B C)=90^{\circ}(\) do \(A B C\) là tam giác vuông tại \(C)\).
Câu hỏi này nằm trong: