Cho hình chóp \(S . A B C D\) có đáy \(A B C D\) là hình vuông cạnh \(a\), tâm \(O, S A \perp(A B C D)\) (như hình vẽ). Mệnh đề nào sau đây là đúng?
A.
\((S B C) \perp(A B C D)\)
B.
\((S B C) \perp(S C D)\)
C.
\((S B C) \perp(S A D)\)
D.
\((S B C) \perp(S A B)\)
Giải thích:
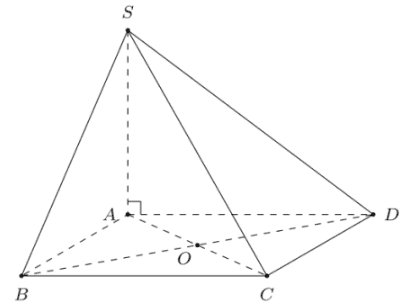
\(\left\{\begin{array}{l}B C \perp S A(\text { do } S A \perp(A B C D)) \\ B C \perp A B(\mathrm{gt}) \\ S A \cap A B=\{A\}\end{array}\right.\)\(\Rightarrow B C \perp(S A B)\) mà \(B C \subset(S B C)\).
Vậy \((S B C) \perp(S A B)\).
Câu hỏi này nằm trong: