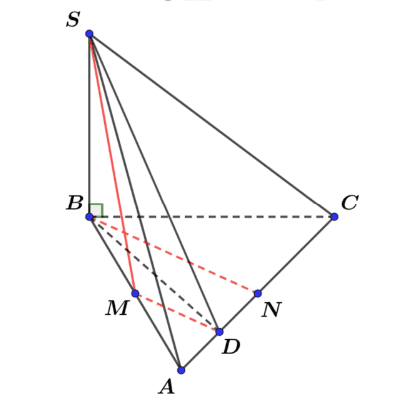
Cho hình chóp \(S . A B C\) có đáy là tam giác đều, cạnh đáy là \(a=4 \sqrt{2} \mathrm{~cm}\), cạnh bên \(S B\) vuông góc với mặt phẳng đáy và \(S B=2 \mathrm{~cm}\). Gọi \(M\) và \(N\) lần lượt là trung điểm của \(A B\) và \(A C\). Số đo góc giữa đường thẳng \(S M\) và \(B N\) bằng bao nhiêu độ?
Giải thích:
Gọi \(D\) là trung diểm của \(A N\).
+) Xét \(\triangle A B N\) có: \(M\) là trung điểm của \(A B\) và \(D\) là trung điểm của \(A N\).
\(\Rightarrow M D\) là đường trung bình của \(\triangle A B N \Rightarrow M D / / B N\).
\(\Rightarrow\) Góc giữa \(S M\) và \(B N\) bằng góc giữa \(S M\) và \(M D\).
+) Xét \(\triangle A B C\) đều có cạnh là \(a=4 \sqrt{2} \mathrm{~cm}, B N\) vừa là trung tuyến vừa là đường cao.
\(\Rightarrow B N=\frac{a \sqrt{3}}{2}=\frac{4 \sqrt{2} \cdot \sqrt{3}}{2}=2 \sqrt{6} \mathrm{~cm}\).
Mà \(M D=\frac{1}{2} B N\) (tính chất đường trung bình) \(\Rightarrow M D=\frac{1}{2} \cdot 2 \sqrt{6}=\sqrt{6} \mathrm{~cm}\).
+) Ta có: \(S B \perp(A B C) \Rightarrow S B \perp B M \Rightarrow \triangle S B M\) là tam giác vuông tại \(B\) \(\Rightarrow S M=\sqrt{S B^{2}+B M^{2}}=\sqrt{2^{2}+\left(\frac{4 \sqrt{2}}{2}\right)^{2}}=2 \sqrt{3} \mathrm{~cm}\).
+) \(\triangle B N D\) vuông tại \(N \Rightarrow B D=\sqrt{B N^{2}+N D^{2}}=\sqrt{(2 \sqrt{6})^{2}+\left(\frac{4 \sqrt{2}}{4}\right)^{2}}=\sqrt{26} \mathrm{~cm}\).
+) \(\triangle S B D\) vuông tại \(B \Rightarrow S D=\sqrt{S B^{2}+B N^{2}}=\sqrt{2^{2}+(\sqrt{26})^{2}}=\sqrt{30} \mathrm{~cm}\).
+) \(\cos \widehat{S M D}=\frac{S M^{2}+M D^{2}-S D^{2}}{2 \cdot S M \cdot M D}=\frac{(2 \sqrt{3})^{2}+(\sqrt{6})^{2}-(\sqrt{30})^{2}}{2 \cdot 2 \sqrt{3} \cdot \sqrt{6}}=-\frac{\sqrt{2}}{2}\)
\(\Rightarrow \widehat{S M D}=\cos ^{-1}\left(-\frac{\sqrt{2}}{2}\right)=135^{\circ}\).
\(\Rightarrow\) Góc giữa đường thẳng \(S M\) và \(B N\) bằng \(180^{\circ}-135^{\circ}=45^{\circ}\).
Câu hỏi này nằm trong: