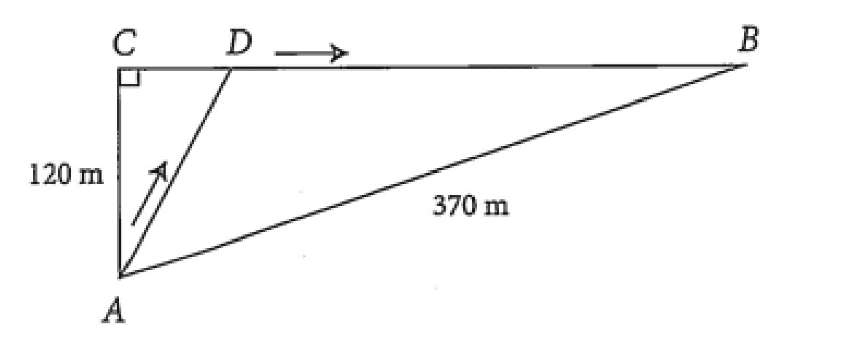
Một chú thỏ ngày nào cũng ra bờ suối ở vị trí \(A\), cách cửa hang của mình tại vị trí \(B\) là \(370 m\) để uống nước, sau đó chú thỏ sẽ đến vị trí \(C\) cách vị trí \(A 120 m\) để ăn cỏ rồi trở về hang. Tuy nhiên, hôm nay sau khi uống nước ở’ bờ suối, chú thỏ không đến vị trí \(C\) như mọi ngày mà chạy đến vị trí \(D\) để tìm cà rốt rồi mới trở về hang (xem hình bên dưới). Biết rằng, tổng thời gian chú thỏ chạy từ vị trí \(A\) đến vị trí \(D\) rồi về hang là 30 giây (không kể thời gian tìm cà rốt), trên đoạn \(A D\) chú thỏ chạy với vận tốc là \(13 \mathrm{~m} / \mathrm{s}\), trên đoạn \(B D\) chú thỏ chạy với vận tốc là \(15 \mathrm{~m} / \mathrm{s}\). Tính khoảng cách giữa hai vị trí \(C\) và \(D\).
Giải thích:
Gọi thời gian chú thỏ chạy trên đoạn \(A D\) là \(x(0\lt x\lt 30)\) (giây), khi đó thời gian chú thỏ chạy trên đoạn \(B D\) là \(30-x\) (giây).
Do đó, quãng đường \(A D\) và \(B D\) lần lượt là \(13 x(m)\) và \(15(30-x)(m)\)
Độ dài quãng đường \(B C\) là: \(\sqrt{370^{2}-120^{2}}=350(\mathrm{~m})\).
Tam giác \(A C D\) vuông tại \(C\) nên \(C D=\sqrt{(13 x)^{2}-120^{2}}(m)\).
Mặt khác, \(C D=B C-B D=350-15(30-x)(m)\).
Do đó, ta có: \(\sqrt{(13 x)^{2}-120^{2}}=350-15(30-x)\).
Giải phương trình này và kết hợp với điều kiện \(0\lt x\lt 30\), ta nhận \(x=10\) (giây).
Vậy khoảng cách giữa vị trí \(C\) và vị trí \(D\) là: \(350-15 \cdot(30-10)=50(\mathrm{~m})\).
Câu hỏi này nằm trong: