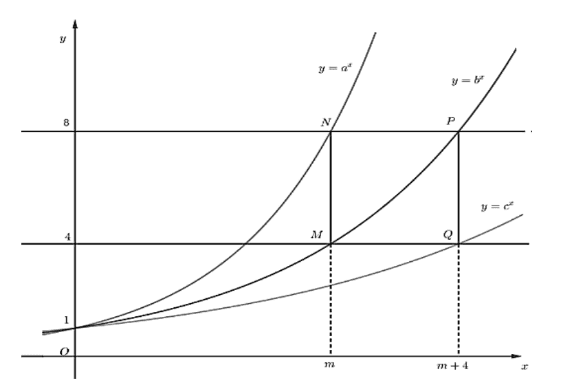
Cho các đường cong \(\left(C_{1}\right): y=a^{x},\left(C_{2}\right): y=b^{x},\left(C_{3}\right): y=c^{x}\) có đồ thị như hình vẽ dưới đây. Biết rằng đường thẳng \(y=8\) cắt các đường \(y=a^{x}, y=b^{x}\) lần lượt tại \(N\) và \(P\), đường thẳng \(y=4\) cắt các đường \(y=b^{x}\) và \(y=c^{x}\) lần lượt tại \(M\) và \(Q\) tạo thành hình vuông \(M N P Q\) có cạnh bằng 4 .Tính giá trị biểu thức \(a^{8} b^{4} c^{6}\).
Giải thích:
Giả sử hoành độ điểm \(M\) là \(m\), ta suy ra \(M(m ; 4) ; N(m ; 8) ; P(m+4 ; 8) ; \mathrm{Q}(m+4 ; 4)\).
Từ giả thiết ta có \(M, P\) thuộc đường cong \(y=b^{x}\) nên \(\left\{\begin{array}{l}b^{m}=4 \\ b^{m+4}=8\end{array} \Leftrightarrow\left\{\begin{array}{l}b^{m}=4 \\ b^{4}=2\end{array} \Leftrightarrow\left\{\begin{array}{l}m=8 \\ b=2^{\frac{1}{4}}\end{array}\right.\right.\right.\)
\(N, Q\) lần lượt thuộc đường cong \(y=a^{x} ; y=c^{x}\) nên \(\left\{\begin{array}{l}a^{8}=8 \\ c^{12}=4\end{array} \Leftrightarrow\left\{\begin{array}{l}a^{8}=2^{3} \\ c^{12}=2^{2}\end{array} \Leftrightarrow\left\{\begin{array}{l}a=2^{\frac{3}{8}} \\ c=2^{\frac{1}{6}}\end{array}\right.\right.\right.\)
Khi đó \(a^{8} b^{4} c^{6}=\left(2^{\frac{3}{8}}\right)^{8} .\left(2^{\frac{1}{4}}\right)^{4}.\left(2^{\frac{1}{6}}\right)^{6}=2^{3+1+1}=2^{5}=32\).
Câu hỏi này nằm trong: