Trong mặt phẳng với hệ toạ độ \(O x y\), cho điểm \(P(-3 ;-2)\) và đường tròn \((C)\) có phương trình \((x-3)^{2}+(y-4)^{2}=36\). Từ điểm \(P\) kẻ các tiếp tuyến \(P M\) và \(P N\) tới đường tròn \((C)\), với \(M, N\) là các tiếp điểm. Phương trình đường thẳng \(M N\) có dạng \(a x+b y-1=0\). Khi đó giá trị của biểu thức \(T=a+2 b\) bằng bao nhiêu?
Giải thích:
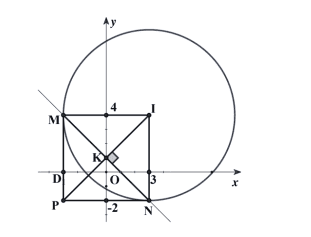
Gọi \(I\) là tâm của đường tròn, ta có tọa độ tâm \(I(3 ; 4)\).
Theo đề ra ta có tứ giác \(I M P N\) là hình vuông, nên đường thẳng \(M N\) nhận \(\overrightarrow{I P}=(-6 ;-6)\) làm véctơ pháp tuyến. Đồng thời đường thẳng \(M N\) đi qua trung điểm \(K(0 ; 1)\) của \(I P\).
Vậy phương trình đường thẳng \(M N: 1 .(x-0)+1 \cdot(y-1)=0\) hay
\(x+y-1=0 \Rightarrow\left\{\begin{array}{l}a=1 \\b=1\end{array}\right. \text {. }\)Khi đó \(T=a+2 b=1+2 \cdot 1=3\).
Câu hỏi này nằm trong: