Một hình chóp cụt đều \(A B C \cdot A^{\prime} B^{\prime} C^{\prime}\) có cạnh đáy lớn bằng \(4 a\), cạnh đáy nhỏ bằng \(2 a\) và chiều cao của nó bằng \(\frac{3 a}{2}\). Tìm thể tích của khối chóp cụt đều đó.
Giải thích:
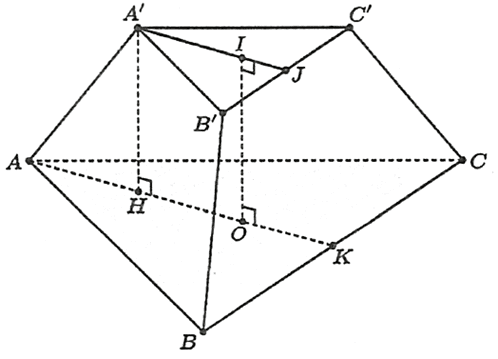
Gọi \(O, I\) theo thứ tự là tâm của đáy lớn \(A B C\) và đáy bé \(A^{\prime} B^{\prime} C^{\prime} ; K, J\) theo thứ tự là trung điểm của \(B C\) và \(B C\).
Ta có \(h=I O=\frac{3 a}{2}\) là chiều cao của hình chóp cụt đều \(A B C \cdot A^{\prime} B^{\prime} C^{\prime}\).
Diện tích hai đáy hình chóp cụt đều là:
\(S_{1}=S_{\triangle A B C}=\frac{(4 a)^{2} \sqrt{3}}{4}=4 a^{2} \sqrt{3} ; S_{2}=S_{\triangle A B^{\prime} C^{\prime}}=\frac{(2 a)^{2} \sqrt{3}}{4}=a^{2} \sqrt{3}\)Thể tích khối chóp cụt đều là:
\(\begin{array}{l}V=\frac{1}{3} h\left(S_{1}+\sqrt{S_{1} S_{2}}+S_{2}\right) \\=\frac{1}{3} \cdot \frac{3 a}{2}\left(4 a^{2} \sqrt{3}+\sqrt{4 a^{2} \sqrt{3} \cdot a^{2} \sqrt{3}}+a^{2} \sqrt{3}\right)=\frac{7 a^{3} \sqrt{3}}{2} \text { (đơn vị thề tích) }\end{array}\)Câu hỏi này nằm trong: