Cho tam thức bậc hai \(f(x)=x^{2}-8 x+7\) có bảng xét dấu như sau:
Tập hợp tất cả các giá trị của \(x\) để \(f(x) \leq 0\) là

A.
\([7 ;+\infty)\)
B.
\([1 ; 7]\)
C.
\((1 ; 7)\)
D.
\((-\infty ; 1]\)
Giải thích:
Ta có bảng xét dấu
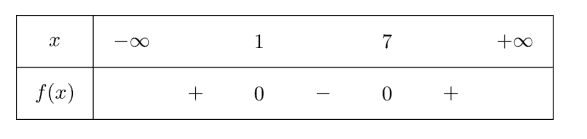
Từ bảng xét dấu ta có \(f(x) \leq 0 \Leftrightarrow x \in[1 ; 7]\).
Câu hỏi này nằm trong: