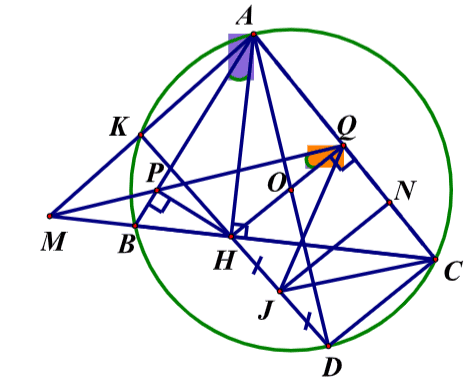
Cho tam giác nhọn \(A B C(A B\lt A C)\) nội tiếp đường tròn \((O)\). Kẻ đường cao \(A H\) của tam giác \(A B C(H\) thuộc \(B C)\). Gọi \(P ; Q\) lần lượt là chân của đường vuông góc kẻ từ \(H\) đến các cạnh \(A B, A C\).
a) Chứng minh \(\widehat{PQH} = \widehat{BAH}\)
Giải thích:
Tứ giác \(A P H Q\) có \(\widehat{APH}=\widehat{AQH}=180^{\circ}\)
Suy ra tứ giác \(A P H Q\) nội tiếp
\(\Rightarrow\) \(\widehat{PQH}=\widehat{PAH}\)
Hay \(\widehat{PQH} = \widehat{BAH}\)
Câu hỏi này nằm trong: