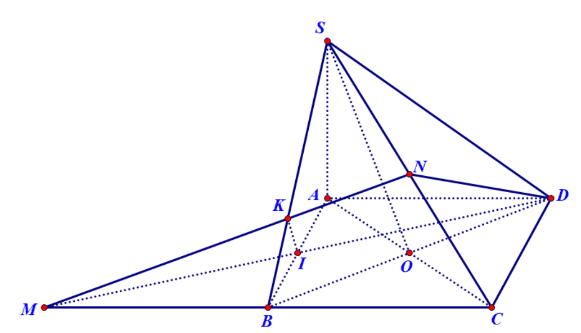
Gọi \(I=D M \cap A B\) và \(K=M N \cap S B\) Ta có: \(B, N\) lần lượt là trung điểm của \(M C, S C\) nên \(K\) là trọng tâm tam giác \(S M C\).Và \(B I\) là đường trung bình của tam giác \(M C D\)

Khi đó \(\frac{V_{M B K I}}{V_{M C N D}}=\frac{M B}{M C} \cdot \frac{M K}{M N} \cdot \frac{M I}{M D}=\frac{1}{2} \cdot \frac{2}{3} \cdot \frac{1}{2}=\frac{1}{6} \Rightarrow V_{M B K I}=\frac{1}{6} V_{M C N D} \Rightarrow V_{B K I C N D}=5 V_{M B K I}\)+) Ta tính thể tích của khối \(S A B C D\) :

\(A B C D\) là hình thoi cạnh \(a\), góc \(\widehat{B A D}=60^{\circ} \Rightarrow \triangle B A D\) đều, cạnh \(a\)

\(\Rightarrow S_{A B C D}=2 S_{A B D}=2 \cdot \frac{a^{2} \sqrt{3}}{4}=\frac{a^{2} \sqrt{3}}{2}\). Mặt khác \([(S B D),(A B C D)]=\widehat{S O A}=45^{\circ} \Rightarrow S A=O A=\frac{a \sqrt{3}}{2}\)

\(\Rightarrow V_{S B C D}=\frac{1}{3} \cdot S A \cdot S_{A B C D}=\frac{1}{3} \cdot \frac{a \sqrt{3}}{2} \cdot \frac{a^{2} \sqrt{3}}{2}=\frac{a^{3}}{4}\)

+) Tính thể tích khối \(K M I B\)

Do đó: \(V_{2}=\frac{5 a^{3}}{48}\) và \(V_{1}=\frac{a^{3}}{4}-\frac{5 a^{3}}{48}=\frac{7 a^{3}}{48} \Rightarrow \frac{V_{1}}{V_{2}}=\frac{7}{5}\).