Cho tam giác \(\mathrm{ABC}, \mathrm{O}\) là trung điểm của \(\mathrm{BC}\). Từ \(\mathrm{B}\) kẻ \(\mathrm{BD}\) vuông góc với \(\mathrm{AC}\)( \(\mathrm{D}\) thuộc \(\mathrm{AC})\). Từ \(\mathrm{C}\) kẻ \(\mathrm{CE}\) vuông góc với \(\mathrm{AB}\) ( \(\mathrm{E}\) thuộc \(\mathrm{AB})\).
a. Chứng minh rằng: \(O D=\frac{1}{2} B C\).
Giải thích:
Vẽ hình (0.5 điểm)
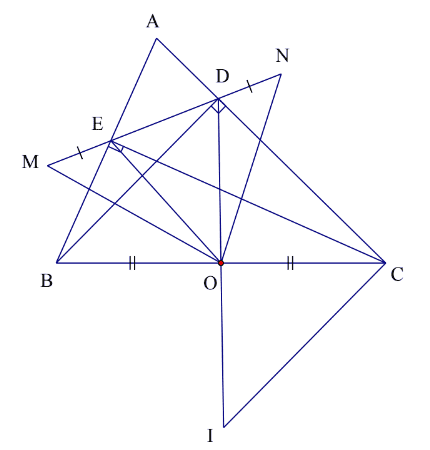
Trên tia đối của tia OD lấy điềm I sao cho \(\mathrm{OI}=\mathrm{OD}\).Nối I với \(\mathrm{C}\).
Chứng minh được \(\triangle \mathrm{OBD}=\triangle \mathrm{OCI}\) (c.g.c)
\(\Rightarrow \mathrm{BD}=\mathrm{CI}\)và \(\angle B D O=\angle O I C\) Mà hai góc này ở vị trí so le trong
\(\Rightarrow \mathrm{DB} / / \mathrm{CI}\)Mà \(\mathrm{CD} \perp \mathrm{BD} \Rightarrow \mathrm{CD} \perp \mathrm{CI}\)
Chứng minh được \(\triangle \mathrm{BDC}=\triangle \mathrm{ICD}\) (c.g.c)
\(\Rightarrow \mathrm{BC}=\mathrm{DI}\)Từ đó \(\Rightarrow O D=\frac{1}{2} B C\).
Câu hỏi này nằm trong: