Cho tứ diện \(A B C D\) có \(C D=a \sqrt{2}, \triangle A B C\) là tam giác đều cạnh \(a, \triangle A C D\) vuông tại \(A\). Mặt phẳng \((B C D)\) vuông góc với mặt phẳng \((A B D)\). Thể tích khối cầu ngoại tiếp tứ diện \(A B C D\) bằng?
A.
\(\frac{4 \pi a^{3}}{3}\).
B.
\(\frac{\pi a^{3} \sqrt{3}}{2}\).
C.
\(\frac{\pi a^{3}}{6}\).
D.
\(4 \pi a^{3}\).
Giải thích:
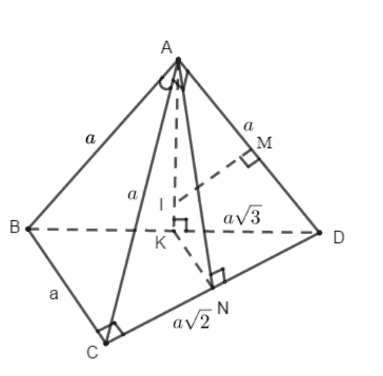
Gọi \(M, N, K\) lần lượt là trung điểm của \(A D\), \(C D, B D\)
\(\triangle A C D\) vuông tại \(A \Rightarrow A D=\sqrt{C D^{2}-A C^{2}}=a\)
\(\Rightarrow \triangle A B D\) cân tại \(A \Rightarrow A K \perp B D\).
Mặt khác \((A B D) \perp(B C D) \Rightarrow A K \perp(B C D)\)
\(\Rightarrow A K \perp C D\) (1).
\(\triangle A C D\) cân tại \(A \Rightarrow A N \perp C D\) (2).
Từ (1) và \((2) \Rightarrow C D \perp K N\)
Mà \(B C / / K N\) (tính chất đường trung bình)
\(\Rightarrow C D \perp B C\)
Suy ra \(K\) là tâm đường tròn ngoại tiếp \(\triangle B C D\).
Đường trung trực của \(A D\) trong mặt phẳng \((A B D)\) cắt \(A K\) tại \(I \Rightarrow I\) là tâm mặt cầu ngoại tiếp tứ diện \(A B C D\).
\(\begin{array}{l}B D=\sqrt{C D^{2}+B C^{2}}=a \sqrt{3}, A K=\sqrt{A D^{2}-K D^{2}}=\sqrt{a^{2}-\frac{3 a^{2}}{4}}=\frac{a}{2} . \\\triangle A K D \sim \triangle A M I(g \cdot g) \Rightarrow \frac{A I}{A D}=\frac{A M}{A K} \Rightarrow R=A I=\frac{A M \cdot A D}{A K}=\frac{a \cdot a}{2 \frac{a}{2}}=a .\end{array}\)Thể tích khối cầu ngoại tiếp tứ diện \(A B C D: V=\frac{4}{3} \pi R^{3}=\frac{4 \pi a^{3}}{3}\).
Câu hỏi này nằm trong: