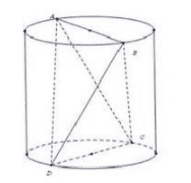
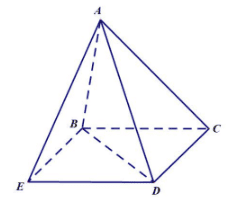
Ta chứng minh công thức: \(V_{A B C D}=\frac{1}{6} A B \cdot C D \cdot d(A B, C D) \cdot \sin (A B, C D)\).

Thật vậy, Lấy điểm \(E\) sao cho tứ giác \(E B C D\) là hình bình hành Khi đó \((A B, C D)=(A B, B E) \Rightarrow \sin (A B, C D)=\sin (A B, B E)\)

Lai có \(d(A B, C D)=d(C D,(A B E))=d(D,(A B E))\)

Ta có: \(V_{A B C D}=V_{A B D E}=\frac{1}{3} d(D,(A B E)) S_{\triangle A B E}=\frac{1}{3} d(A B, C D) \cdot \frac{1}{2} A B \cdot B E \cdot \sin (A B, B E)\).

Mà \(B E=C D\)Vậy, \(V_{A B C D}=\frac{1}{6} A B \cdot C D \cdot d(A B, C D) \cdot \sin (A B, C D)\).

Suy ra \(d(A B, C D)=\frac{6 V_{A B C D}}{A B \cdot C D \cdot \sin 30^{\circ}}=\frac{180}{6 \cdot 6 \cdot \frac{1}{2}}=10\).

Chiều cao của lăng trụ là \(h=d(A B, C D)=10\).

Thể tích lăng trụ là \(V=\pi r^{2} h=\pi \cdot 3^{2} \cdot 10=90 \pi\).