Cho hình hộp \(A B C D \cdot A^{\prime} B^{\prime} C^{\prime} D^{\prime}\) có 6 mặt là hình vuông cạnh \(a\). Khi đó:
d) \(\widehat{B C^{\prime} D}=90^{\circ}\)
A.
True
B.
False
Giải thích:
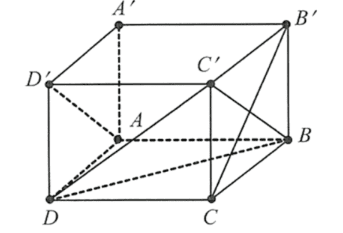
Ta có: \(B C^{\prime} / / A D^{\prime}\) nên \(\left(A D^{\prime}, B^{\prime} C\right)=\left(B C^{\prime}, B^{\prime} C\right)=90^{\circ}\).
Ta có: \(B C^{\prime} / / A D^{\prime}\) nên \(\left(A D^{\prime}, D C^{\prime}\right)=\left(B C^{\prime}, D C^{\prime}\right)=\widehat{B C^{\prime} D}\)
Ta có: \(\triangle B C^{\prime} D\) đều nên \(\widehat{B C^{\prime} D}=60^{\circ}\).
Câu hỏi này nằm trong: