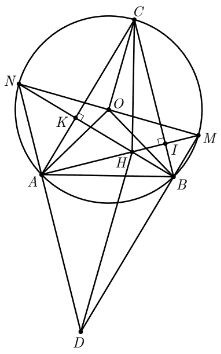
Cho đường tròn \((O)\), hai điểm \(A, B\) nằm trên \((O)\) sao cho \(\widehat{A O B}=90^{\circ}\). Điểm \(C\) nằm trên cung lớn \(A B\) sao cho \(A C\gt B C\) và tam giác \(A B C\) có ba góc đều nhọn. Các đường cao \(A I, B K\) của tam giác \(A B C\) cắt nhau tại điểm \(H . B K\) cắt \((O)\) tại điểm \(N\) (khác điểm \(B\)); \(A I\) cắt \((O)\) tại điểm \(M\) (khác điểm \(A\)); \(NA\) cắt \(M B\) tại điểm \(D\). Chứng minh rằng:
b) \(MN\) là đường kính của đường tròn \((O)\)
Giải thích:
Do tứ giác \(C I H K\) nội tiếp nên
\(\begin{array}{l}45^{\circ}=\text{cung } I C K=\text{cung } B H I=\frac{1}{2} \angle \text{cung } B M+\frac{1}{2} \angle \text{cung } A N . \\\Rightarrow \angle \text{cung } B M+\angle \text{cung } A N=90^{\circ} .\end{array}\)
Suy ra, \(\angle \text{cung } M N=\angle \text{cung } A B+(\angle \text{cung } B M+\angle \text{cung } A N)\)
\(=90^{\circ}+90^{\circ}=180^{\circ}\) hay
\(M N\) là đường kính của \((O)\).
Câu hỏi này nằm trong: