Cho hai số thực dương \(a, b\) thỏa mãn hệ thức: \(2 \log _{2} a-\log _{2} b \leq \log _{2}(a+6 b)\). Tìm giá trị lớn nhất \(P_{\text {Max }}\) của biểu thức \(P=\frac{a b-b^{2}}{a^{2}-2 a b+2 b^{2}}\).
A.
\(P_{M a x}=\frac{2}{3}\)
B.
\(P_{M a x}=0\)
C.
\(P_{M a x}=\frac{1}{2}\)
D.
\(P_{\text{Max}}=\frac{2}{5}\)
Giải thích:
Ta có: \(2 \log _{2} a-\log _{2} b \leq \log _{2}(a+6 b) \Leftrightarrow \log _{2} a^{2} \leq \log _{2}\left(a b+6 b^{2}\right) \Leftrightarrow a^{2} \leq a b+6 b^{2}\)
\(\Leftrightarrow\left(\frac{a}{b}\right)^{2}-\frac{a}{b}-6 \leq 0 \Leftrightarrow-2 \leq \frac{a}{b} \leq 3\).
Do \(a, b\) dương nên \(0\lt \frac{a}{b} \leq 3\).
Đặt \(t=\frac{a}{b}, 0\lt t \leq 3\).
Khi đó: \(P=\frac{a b-b^{2}}{a^{2}-2 a b+2 b^{2}}=\frac{t-1}{t^{2}-2 t+2}\)
Xét hàm số \(f(t)=\frac{t-1}{t^{2}-2 t+2}\) với \(0\lt t \leq 3\).
Ta có: \(f^{\prime}(t)=\frac{-t^{2}+2 t}{\left(t^{2}-2 t+2\right)^{2}}, \ t \in(0 ; 3]\).
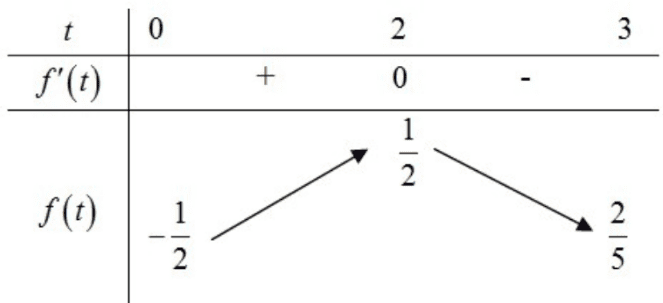
Suy ra \(f(t) \leq f(2)=\frac{1}{2}\). Vậy \(\underset{(0 ; 2]}{\text{Max}} f(t)=\frac{1}{2}\) khi \(t=2\).
Do đó \(P_{M a x}=\frac{1}{2}\).
Câu hỏi này nằm trong: