Một nhà sử học đến du lịch Đại kim tự tháp Giza (Ai Cập). Hướng dẫn viên du lịch cung cấp thông tin về Đại kim tự tháp này có dạng hình chóp tứ giác đ...

Question

Accepted Answer

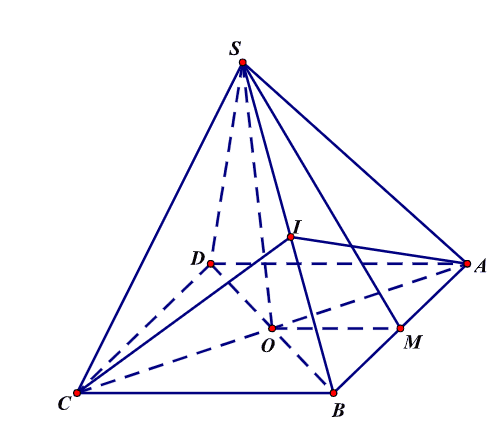
+ Gọi hình chóp tứ giác đều là $S . A B C D$ như hình vẽ, $O=A C \cap B D, M$ là trung điểm của $A B$

Khi đó góc nhị diện tạo bởi mặt bên $(S A B)$ và mặt đáy $(A B C D)$ là $[S, A B, O]$.

Ta có $S M \perp A B$ và $O M \perp A B$

Suy ra $SM O$ là góc phẳng nhị diện $[S, A B, O$ ].

Ta có $\tan S H=\frac{S O}{O M} \Rightarrow B C=2 O M=\frac{2 S O}{\tan S M O} \approx 230,36(\mathrm{~m})$

+ Tìm số đo của góc phẳng nhị diện hai mặt bên, tức là số đo của góc phẳng nhị diện $[A, S B, C]$

Kẻ $A I \perp S B$, lại có $S B \perp A C$ (vì $A C \perp(S B D)$ ) từ đó suy ra $S B \perp C I$.

Vậy góc phẳng nhị diện $[A, S B, C]$ là góc $A{H} C$.

Hai tam giác $\triangle S A B=\triangle S B C$ suy ra hai đường cao $A I=C I$, tam giác $\triangle I A C$ cân tại $I$.

Đặt $a=230,36 ; h=146,6$

$\begin{array}{l}\text { Ta có } A C=a \sqrt{2} \Rightarrow O A=\frac{a \sqrt{2}}{2} \Rightarrow S A=\sqrt{S O^{2}+O A^{2}}=\sqrt{h^{2}+\frac{a^{2}}{2}} ; \S M=\sqrt{S O^{2}+O M^{2}}=\sqrt{h^{2}+\frac{a^{2}}{4}}\end{array}$$S_{\triangle S A B}=\frac{1}{2} A I. S B=\frac{1}{2} S M .A B \Rightarrow A I=\frac{S M. A B}{S B}=\frac{\sqrt{h^{2}+\frac{a^{2}}{4}} . a}{\sqrt{h^{2}+\frac{a^{2}}{2}}}$$\begin{array}{l}\cos A+C=\frac{A I^{2}+C I^{2}-A C^{2}}{2 A I . C I}=\frac{2 a^{2}\left(\frac{4 h^{2}+a^{2}}{2\left(2 h^{2}+a^{2}\right)}\right)-2 a^{2}}{2 \cdot \frac{4 h^{2}+a^{2}}{2\left(2 h^{2}+a^{2}\right)} a^{2}}=\frac{-a^{2}}{4 h^{2}+a^{2}} \text {, thay số } \a=230,36 ; h=146,6 \\end{array}$

Ta suy ra được $A F C \approx 112^{\circ} 26^{\prime} 16^{\prime \prime}$.

Đề thi giữa kì 2 (Cấu trúc mới) - KNTT - Đề số 8 - MĐ 9978