Trong hình hộp \(A B C D .A^{\prime} B^{\prime} C^{\prime} D^{\prime}\) có tất cả các cạnh đều bằng nhau. Trong các mệnh đề sau, mệnh đề nào sai?
A.
\(B B^{\prime} \perp B D\)
B.
\(A^{\prime} C^{\prime} \perp B D\)
C.
\(A^{\prime} B \perp D C^{\prime}\)
D.
\(B C^{\prime} \perp A^{\prime} D\)
Giải thích:
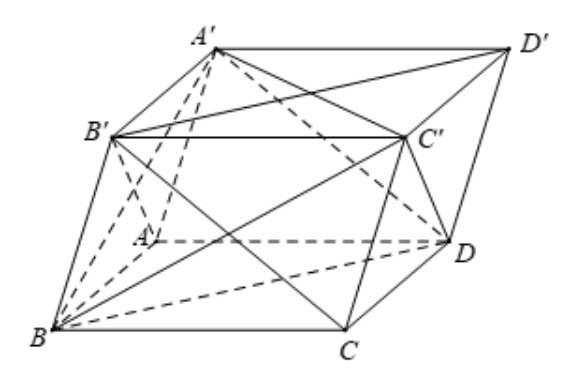
Vì hình hộp \(A B C D \cdot A^{\prime} B^{\prime} C^{\prime} D^{\prime}\) có tất cả các cạnh đều bằng nhau nên các tứ giác \(A B C D\), \(A^{\prime} B^{\prime} B A, B^{\prime} C^{\prime} C B\) đều là hình thoi
Ta có\(A C \perp B D\) mà \(A C / / A^{\prime} C^{\prime} \Rightarrow A^{\prime} C^{\prime} \perp B D\) (B đúng).
\(A^{\prime} B \perp A B^{\prime}\) mà \(A B^{\prime} / / D C^{\prime} \Rightarrow A^{\prime} B \perp D C^{\prime}\) (C đúng).
\(B C^{\prime} \perp B^{\prime} C\) mà \(B^{\prime} C / / A^{\prime} D \Rightarrow B C^{\prime} \perp A^{\prime} D\) (D đúng).
Câu hỏi này nằm trong: