Cho tứ diện \(A B C D\) có \(A B=A C, D B=D C\). Gọi \(I\) là trung điểm của \(B C\). Khi đó:
a) \(B C \perp A I\)
A.
True
B.
False
Giải thích:
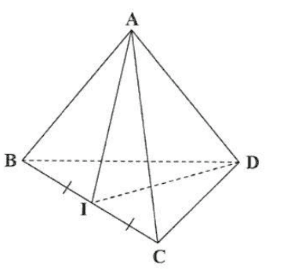
Ta có \(B C \perp A I\) (vì \(A B=A C\) )\(B C \perp D I\) (vì \(B D=C D) \Rightarrow B C \perp(A D I)\)
Ta có \(\left\{\begin{array}{l}B C \perp(A D I) \\ A D \subset(A D I)\end{array} \Rightarrow B C \perp A D\right.\)
Ta có \(A I=A D \Rightarrow A H \perp D I\)
Mặt khác \(A H \perp B C\) (do \(B C \perp(A D I)) \Rightarrow A H \perp(B C D)\)
Vậy \(H\) là hình chiếu vuông góc của \(A\) trên \((B C D)\).
Câu hỏi này nằm trong: