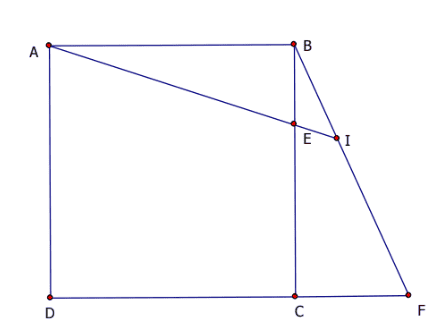
1. Cho hình vuông \(A B C D ; E, F, I\) là các điểm xác định bởi \(\overrightarrow{B E}=\frac{1}{3} \overrightarrow{B C}\), \(\overrightarrow{C F}=-\frac{1}{2} \overrightarrow{C D}, \overrightarrow{B I}=\frac{2}{5} \overrightarrow{B F}\).

Chứng minh rằng \(A, E, I\) thẳng hàng và góc \(A I C=90^{\circ}\).

Đặt \(\overrightarrow{A B}=\vec{u} ; \overrightarrow{A D}=\vec{v}\), ta có: \(\overrightarrow{A E}=\overrightarrow{A B}+\overrightarrow{B E}=\vec{u}+\frac{1}{3} \vec{v}\)

Từ \(\overrightarrow{B I}=\frac{2}{5} \overrightarrow{B F} \Rightarrow \overrightarrow{A I}-\overrightarrow{A B}=\frac{2}{5}(\overrightarrow{A F}-\overrightarrow{A B}) \Leftrightarrow \overrightarrow{A I}-\overrightarrow{A B}=\frac{2}{5}(\overrightarrow{A D}+\overrightarrow{D F}-\overrightarrow{A B})\)Hay:\(\overrightarrow{A I}-\vec{u}=\frac{2}{5}\left(\vec{v}+\frac{3}{2} \vec{u}-\vec{u}\right) \Leftrightarrow \overrightarrow{A I}=\frac{6}{5} \vec{u}+\frac{2}{5} \vec{v}\)

Như vậy \(\overrightarrow{A I}=\frac{6}{5} \overrightarrow{A E}\) nên ba điểm \(A, E, I\) thẳng hàng.

Ta có:

Do \(A B C D\) là hình vuông nên: \(\vec{u}^{2}=\vec{v}^{2} ; \vec{u} \cdot \vec{v}=0\)

Bởi vậy:

Suy ra \(A I C=90^{\circ}\)