Cho khối tứ diện \(O A B C\) có \(O A, O B, O C\) đôi một vuông góc và \(O A=3 \mathrm{~cm}, O B=4 \mathrm{~cm}, O C=10 \mathrm{~cm}\). Thể tích khối tứ diện \(O A B C\) bằng
A.
\(20 \mathrm{~cm}^{3}\)
B.
\(10 \mathrm{~cm}^{3}\)
C.
\(40 \mathrm{~cm}^{3}\)
D.
\(120 \mathrm{~cm}^{3}\)
Giải thích:
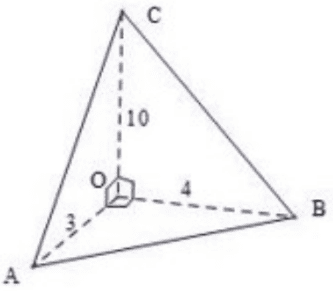
Ta có: \(\left\{\begin{array}{l}O C \perp O A \\ O C \perp O B\end{array} \Rightarrow O C \perp(O A B)\right.\).
Do đó \(V_{C O A B}=\frac{1}{3} \cdot S_{O A B} \cdot O C=\frac{1}{6} \cdot O A \cdot O B \cdot O C=\frac{1}{6} \cdot 3 \cdot 4 \cdot 10=20 \mathrm{~cm}^{3}\).
Câu hỏi này nằm trong: