Cho hình chóp \(S . A B C\) có \(S A\) vuông góc với đáy, hai mặt phẳng \((S A B)\) và \((S B C)\) vuông góc với nhau, \(S B=a \sqrt{3}\), góc giữa \(S C\) và \((S A B)\) là \(45^{\circ}\) và \(A S B=30^{\circ}\).
c) Hai đường thẳng \(A B\) và \(C B\) vuông góc với nhau.
A.
B.
Giải thích:
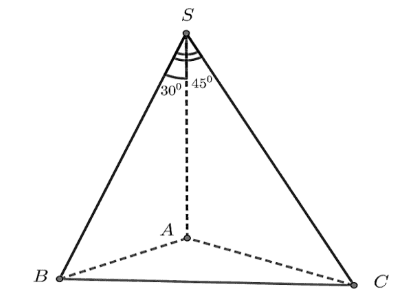
Theo giả thiết, \(\triangle S A B\) vuông tại \(A\) có \(S B=a \sqrt{3}, A S B=30^{\circ}\).
Khi đó, \(S A=S B. \cos 30^{\circ}=\frac{3 a}{2}\) và \(A B=S B .\sin 30^{\circ}=\frac{a \sqrt{3}}{2}\).
Do \(S A \perp(A B C)\) nên \((S A B) \perp(A B C)\).
Vậy hai mặt phẳng \((S B C)\) và \((A B C)\) cùng vuông góc với \((S A B)\) nên suy ra \(B C \perp(S A B) \Rightarrow(S C,(S A B))=(S C, S B)=C S B=45^{\circ}\).
Suy ra \(\triangle S B C\) vuông cân tại \(B \Rightarrow B C=S B=a \sqrt{3}\).
Mặt khác, \(B C \perp(S A B) \Rightarrow C B \perp A B \Rightarrow \triangle A B C\) vuông tại \(B\).
Khi đó, \(S_{\triangle A B C}=\frac{1}{2} A B.B C=\frac{3 a^{2}}{4}\)
Câu hỏi này nằm trong: