Cho tứ diện \(O A B C\) có \(O A, O B, O C\) đôi một vuông góc với nhau. Gọi \(O K\) là đường cao của tam giác \(O B C\) và \(O H\) là đường cao của tam giác \(O A K\). Khi đó:
c) Các cạnh đối nhau trong tứ diện \(O A B C\) thì vuông góc với nhau.
A.
B.
Giải thích:
Ta có:
\[\begin{array}{l}\left\{\begin{array}{l}O A \perp O B \\O A \perp O C\end{array} \Rightarrow O A \perp(O B C) ;\right. \\\left\{\begin{array}{l}O B \perp O A \\O B \perp O C\end{array} \Rightarrow O B \perp(O A C) ;\right.\end{array}\]Vì \(O A \perp(O B C)\) mà \(B C \subset(O B C) \Rightarrow O A \perp B C\).
Vì \(O B \perp(O A C)\) mà \(A C \subset(O A C) \Rightarrow O B \perp A C\).
Ta có: \(\left\{\begin{array}{l}O C \perp O A \\ O C \perp O B\end{array} \Rightarrow O C \perp(O A B)\right.\), mà \(A B \subset(O A B) \Rightarrow O C \perp A B\).
Vậy các cặp cạnh đối nhau của tứ diện \(O A B C\) vuông góc với nhau.
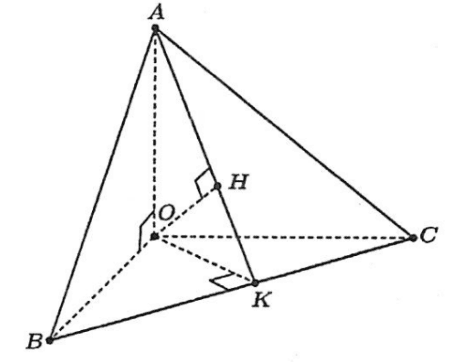
Ta có: \(\left\{\begin{array}{l}B C \perp O K \\ B C \perp O A(\text { do } O A \perp(O B C))\end{array} \Rightarrow B C \perp(O A K)\right.\);mà \(O H \subset(O A K) \Rightarrow O H \perp B C\).
Khi đó: \(\left\{\begin{array}{l}O H \perp A K \\ O H \perp B C \\ A K \cap B C=K \\ A K, B C \subset(A B C)\end{array} \Rightarrow O H \perp(A B C)\right.\).
Câu hỏi này nằm trong: