Trong hình hộp \(A B C D \cdot A^{\prime} B^{\prime} C^{\prime} D^{\prime}\) có tất cả các cạnh đều bằng nhau. Khi đó:
c) \(A^{\prime} B \perp D C^{\prime}\).
A.
B.
Giải thích:
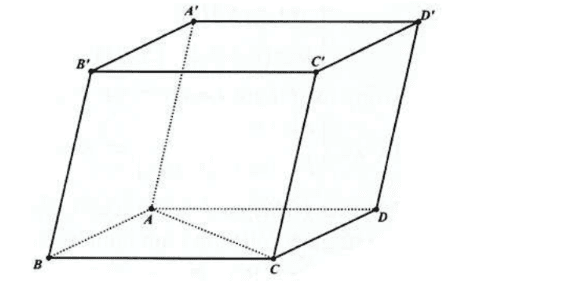
Vì hình hộp \(A B C D \cdot A^{\prime} B^{\prime} C^{\prime} D^{\prime}\) có tất cả các cạnh đều bằng nhau nên các tứ giác \(A B C D, A^{\prime} B^{\prime} B A, B^{\prime} C^{\prime} C B\) đều là hình thoi.
\(\begin{array}{l}A C \perp B D \text { mà } A C / / A^{\prime} C^{\prime} \Rightarrow A^{\prime} C^{\prime} \perp B D \text {. } \\ A^{\prime} B \perp A B^{\prime} \text { mà } A B^{\prime} / / D C^{\prime} \Rightarrow A^{\prime} B \perp D C^{\prime} \text {. }\end{array}\)
\(B C^{\prime} \perp B^{\prime} C\) mà \(B^{\prime} C / / A^{\prime} D \Rightarrow B C^{\prime} \perp A^{\prime} D\).
Câu hỏi này nằm trong: