Cho hình chóp \(S . A B C D\) có đáy \(A B C D\) là hình thoi tâm \(O\), cạnh \(a\). Biết \(S A=S B=S C=a\). Đặt \(S D=x(0\lt x\lt a \sqrt{3})\).
b) Tính \(x\) theo \(a\) sao cho tích \(A C . S D\) lớn nhất.
Giải thích:
Cách 1:
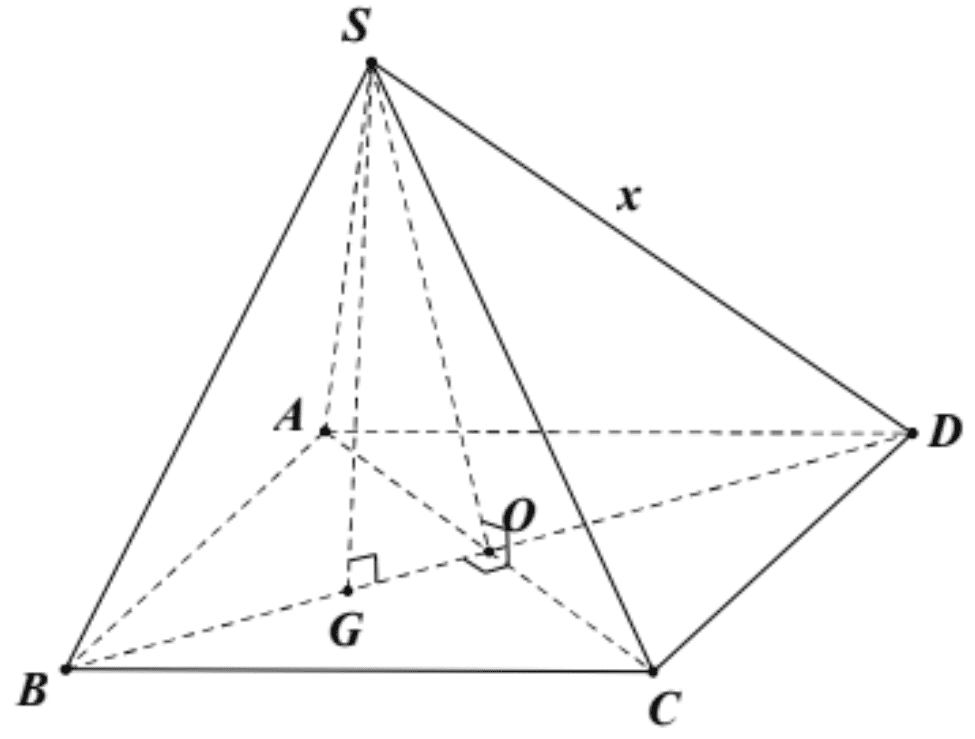
Gọi \(G\) là tâm đường tròn ngoại tiếp tam giác \(A B C\).
Do \(S A=S B=S C \Rightarrow S G \perp(A B C D)\).
Ta có: \(\left\{\begin{array}{l}A C \perp B D \\ A C \perp S G\end{array} \Rightarrow A C \perp(S B D) \Rightarrow A C \perp S O\right.\).\(\triangle S O C=\triangle B O C\) (do \(S C=B C=a, O C\) chung)
\(S O=O B=O D \Rightarrow \triangle B S D\) vuông tại \(S\).
\(B D^{2}=a^{2}+x^{2} \Rightarrow O D=\frac{\sqrt{a^{2}+x^{2}}}{2}\).
\(O A^{2}=A D^{2}-O D^{2}=a^{2}-\frac{a^{2}+x^{2}}{4}=\frac{3 a^{2}-x^{2}}{4}\).
\(\Rightarrow O A=\frac{\sqrt{3 a^{2}-x^{2}}}{2} \Rightarrow A C=\sqrt{3 a^{2}-x^{2}}\).
Xét \(A C . S D=x \cdot \sqrt{3 a^{2}-x^{2}} \leq \frac{x^{2}+3 a^{2}-x^{2}}{2}=\frac{3 a^{2}}{2}\).
Dấu " \(=\) " xảy ra khi \(x=\sqrt{3 a^{2}-x^{2}} \Leftrightarrow 2 x^{2}=3 a^{2} \Leftrightarrow x^{2}=\frac{3 a^{2}}{2} \Leftrightarrow x=\frac{a \sqrt{3}}{\sqrt{2}}=\frac{a \sqrt{6}}{2}\).
Cách 2:
Gọi \(I\) là hình chiếu vuông góc của \(S\) trên mặt phẳng \((A B C D)\), do \(S A=S B=S C=a\) nên \(I\) là tâm đường tròn ngoại tiếp tam giác \(A B C\), dễ thấy \(I\) thuộc đường thẳng \(B O\).
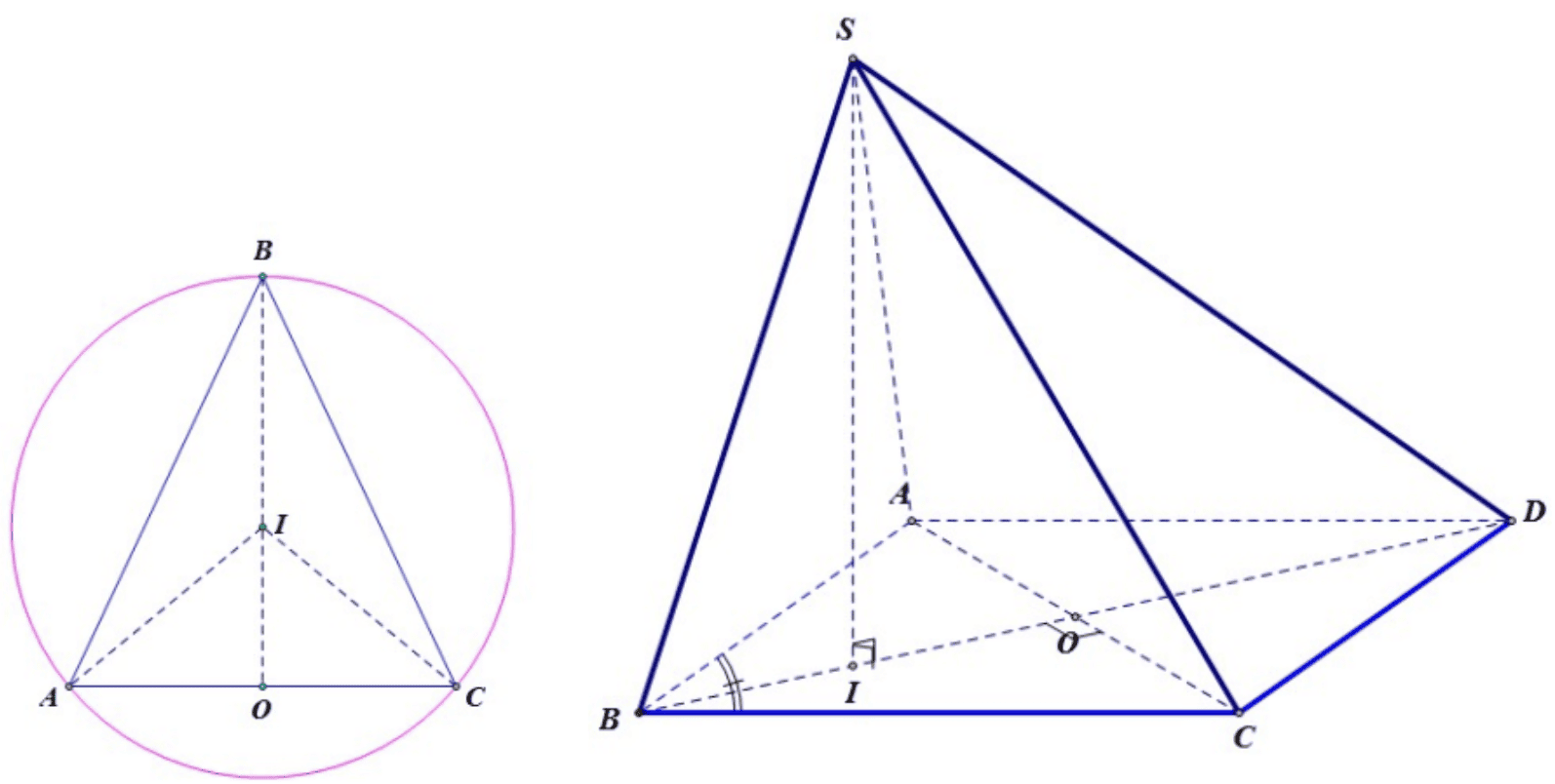
Đặt \(\widehat{A B C}=\alpha\). Ta có \(A C=2 R \sin \alpha\). Suy ra
\(B O=\sqrt{a^{2}-R^{2} \sin ^{2} \alpha} .\)Theo công thức tính diện tích tam giác \(A B C\) ta có: \(\frac{1}{2} \cdot a^{2} \cdot \sin \alpha=\frac{1}{2} \cdot \sqrt{a^{2}-R^{2} \cdot \sin ^{2} \alpha} \cdot 2 R \sin \alpha\)
\(\Leftrightarrow a^{2}=4 R^{2}\left(a^{2}-R^{2} \cdot \sin ^{2} \alpha\right) \Rightarrow \sin \alpha=\frac{a \sqrt{4 R^{2}-a^{2}}}{2 R^{2}} \text {. }\)Mặt khác xét tam giác vuông \(S B I\) và tam giác vuông \(S I D\) ta có:
\(S I^{2}=a^{2}-R^{2}=x^{2}-\left(2 \sqrt{a^{2}-R^{2} \sin ^{2} \alpha}-R\right)^{2} \text {. }\)Thay \(\sin \alpha=\frac{a \sqrt{4 R^{2}-a^{2}}}{2 R^{2}}\) vào rút gọn ta được \(R=\frac{a^{2}}{\sqrt{a^{2}+x^{2}}}\).
Nên \(A C=2 R \sin \alpha=\sqrt{3 a^{2}-x^{2}}\). Từ đó \(A C \cdot S D=x \sqrt{3 a^{2}-x^{2}}=\sqrt{-x^{4}+3 a^{2} x^{2}}\).
Xét hàm số \(f(x)=-x^{4}+3 a^{2} x^{2}\) với \((0\lt x\lt a \sqrt{3})\).
Có \(f^{\prime}(x)=-4 x^{3}+6 a^{2} x=0 \Leftrightarrow\left[\begin{array}{l}x=0 \\ x= \pm \frac{\sqrt{6} a}{2}\end{array}\right.\) do \(x \in(0 ; \sqrt{3} a)\) nên ta nhận \(x=\frac{\sqrt{6}}{2} a\).
Lập bảng biến thiên ta được \(\max _{(0 ; \sqrt{3} a)} f(x)=f\left(\frac{\sqrt{6}}{2} a\right)\)
Vậy khi \(x=\frac{\sqrt{6}}{2} a\) thì \(A C . S D\) đạt giá trị lớn nhất.
Câu hỏi này nằm trong: