Cho tam giác \(A B C\) có cạnh \(B C=10\), góc \(A B C\) bằng \(60^{\circ}\). Trên cạnh \(A B\) ta lấy điểm \(M\) sao cho \(A M=3\) (như hình vẽ). Tính độ dài đoạn thẳng \(B M\) biết rằng \(C M=\frac{8}{9} C A\) (đáp số gần đúng đến hàng phần trăm).
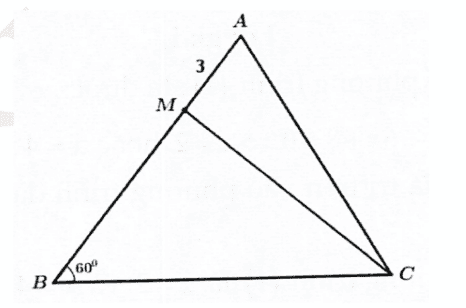
Giải thích:
Đặt \(B M=x(x \geq 0)\).
Ta có \(A C=\sqrt{A N^{2}+N C^{2}-2 A N \cdot N C \cdot \cos 60^{\circ}}=\sqrt{x^{2}+100-10 x}\)
\(C M=\sqrt{B M^{2}+B C^{2}-2 B M \cdot B C \cdot \cos 60^{\circ}}=\sqrt{(x+3)^{2}+100-10(x+3)}\)\(=\sqrt{x^{2}-4 x+79}\)Theo đề bài ta có: \(A C=\frac{8}{9} B C \Rightarrow \sqrt{x^{2}-10 x+100}=\frac{8}{9} \sqrt{x^{2}-4 x+79}\)
\(\begin{array}{l}\Rightarrow 81\left(x^{2}-10 x+100\right)=64\left(x^{2}-4 x+79\right) \\\Rightarrow 17 x^{2}-554 x+3044=0 \Rightarrow x \approx 25,59 \text { hoặc } x \approx 6,99 \text {. }\end{array}\)Vậy \(B M \approx 25,59\) hoặc \(B M \approx 6,99\).
Câu hỏi này nằm trong: