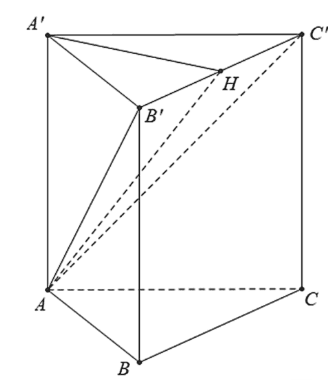
Gọi \(H\) là trung điểm của \(B^{\prime} C^{\prime}\), do các tam giác \(\Delta A^{\prime} B^{\prime} C^{\prime}, \Delta A B^{\prime} C^{\prime}\) lần lượt cân đỉnh \(A^{\prime}\) và \(A\) nên \(A H \perp B^{\prime} C^{\prime}, A^{\prime} H^{\prime} \perp B^{\prime} C^{\prime}\)

Suy ra: \(\widehat{\left.\left(A B^{\prime} C^{\prime}\right),(A B C)\right)}=\widehat{\left(\left(A B^{\prime} C^{\prime}\right),\left(A^{\prime} B^{\prime} C^{\prime}\right)\right)}=\widehat{\left(A H, A^{\prime} H\right)}=\widehat{A H A^{\prime}}\)

Xét tam giác: \(A H A^{\prime}\) có \(\widehat{A}^{\prime}=90^{\circ}, A^{\prime} H=a \sqrt{3}\) và \(\tan \widehat{A H A^{\prime}}=\frac{A A^{\prime}}{A^{\prime} H}=\frac{1}{\sqrt{3}} \Rightarrow \widehat{A H A^{\prime}}=30^{\circ}\).

Vậy số đo góc tạo bởi hai mặt phẳng \(\left(A B^{\prime} C^{\prime}\right)\) và \((A B C)\) bằng \(30^{\circ}\).