Ông An có một mảnh đất hình vuông diện tích \(100 \mathrm{~m}^{2}\). Ông muốn chia làm 3 phần, một nửa mảnh đất là để xây nhà \((A B F E)\) phần còn lại làm vườn, trồng rau và hoa, trong đó phần trồng hoa là một hình tròn tiếp xúc với cạnh \(E F\), cạnh \(C D\) và đường đi \(D O\). Xác định vị trí tâm của phần đất trồng hoa.
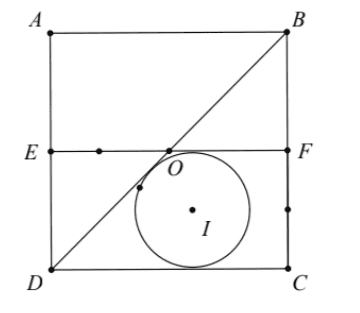
Giải thích:
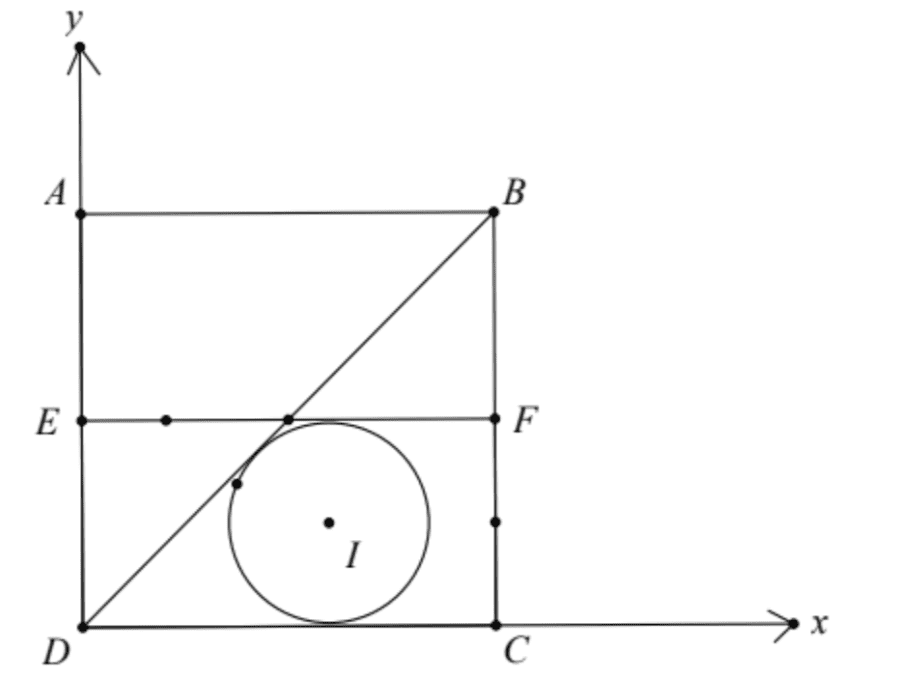
Chọn hệ trục tọa độ như hình vẽ.
Khi đó: \(D(0 ; 0) ; C(10 ; 0) ; B(10 ; 10) ; A(0 ; 10) ; E(0 ; 5) ; F(10 ; 5)\).
Đường thẳng \(B D\) có phương trình \(x-y=0\).
Đường tròn tâm \(I\) tiếp xúc với \(D C\) và \(E F\) nên có bán kính là \(R=\frac{5}{2}\) và \(I\) có tung độ bằng \(\frac{5}{2}\).
Gọi tọa độ \(I=\left(a ; \frac{5}{2}\right), 0\lt a\lt 10\).
Ta có: \(d(I, B D)=\frac{5}{2} \Leftrightarrow \frac{\left|a-\frac{5}{2}\right|}{\sqrt{2}}=\frac{5}{2} \Leftrightarrow\left[\begin{array}{l}a=\frac{5 \sqrt{2}}{2}+\frac{5}{2} \approx 6.04 \\ a=\frac{5}{2}-\frac{5 \sqrt{2}}{2}(l)\end{array}\right.\)
Vậy tọa độ tâm hình tròn trồng hoa là \(I(6,04 ; 2,5)\).
Câu hỏi này nằm trong: