Trong không gian với hệ trục tọa độ \(\mathrm{Oxyz}\),cho tứ diện \(\mathrm{ABCD}\) có điểm \(A(1 ; 1 ; 1), B(2 ; 0 ; 2)\), \(C(-1 ;-1 ; 0), D(0 ; 3 ; 4)\). Trên các cạnh \(A B, A C, A D\) lần lượt lấy các điểm \(B^{\prime}, C^{\prime}, D^{\prime}\) thỏa: \(\frac{A B}{A B^{\prime}}+\frac{A C}{A C^{\prime}}+\) \(\frac{A D}{A D^{\prime}}=4\). Viết phương trình mặt phẳng \(\left(B^{\prime} C^{\prime} D^{\prime}\right)\) biết tứ diện \(A B^{\prime} C^{\prime} D^{\prime}\) có thể tích nhỏ nhất?
A.
\(16 x+40 y+44 z-39=0\).
B.
\(16 x-40 y-44 z+39=0\).
C.
\(16 x+40 y-44 z+39=0\).
D.
\(16 x-40 y-44 z-39=0\).
Giải thích:
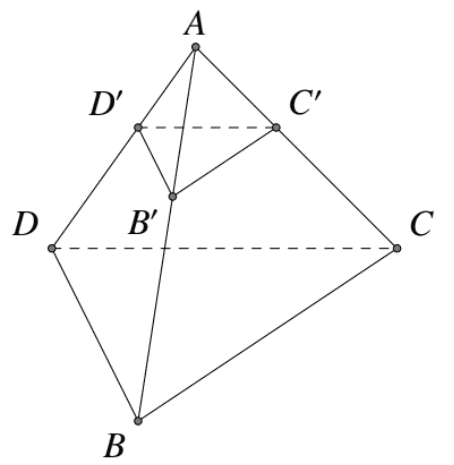
\(\frac{V_{A B C D}}{V_{A B^{\prime} C^{\prime} D^{\prime}}}=\frac{A B}{A B^{\prime}} \cdot \frac{A C}{A C^{\prime}} \cdot \frac{A D}{A D^{\prime}} \leq\left(\frac{\frac{A B}{A B^{\prime}}+\frac{A C}{A C^{\prime}}+\frac{A D}{A D^{\prime}}}{3}\right)^{3}=\frac{64}{27}\)
\(\Rightarrow V_{A B^{\prime} C^{\prime} D^{\prime}} \geq \frac{27}{64} V_{A B C D}\).
Dấu = xảy ra khi: \(\frac{A B}{A B^{\prime}}=\frac{A C}{A C^{\prime}}=\frac{A D}{A D^{\prime}}=\frac{4}{3}\).
Suy ra \(\left\{\begin{array}{l}\left(B^{\prime} C^{\prime} D^{\prime}\right) \|(B C D) \\ \overrightarrow{A B^{\prime}}=\frac{3}{4} \overrightarrow{A B} .\end{array}\right.\)
Ta có \(\left\{\begin{array}{l}\overrightarrow{B C}=(-3 ;-1 ;-2) \\ \overrightarrow{B D}=(-2 ; 3 ; 2)\end{array} \Rightarrow \vec{n}_{\left(B^{\prime} C^{\prime} D^{\prime}\right)}=(4 ; 10 ;-11)\right.\).
Mặt khác \(\overrightarrow{A B^{\prime}}=\frac{3}{2} \overrightarrow{A B}=\left(\frac{3}{4} ;-\frac{3}{4} ; \frac{3}{4}\right) \Rightarrow B^{\prime}\left(\frac{7}{4} ; \frac{1}{4} ; \frac{7}{4}\right)\).
Vậy phương trình mặt phẳng \(\left(B^{\prime} C^{\prime} D^{\prime}\right)\) là \(16 x+40 y-44 z+39=0\).
Câu hỏi này nằm trong: