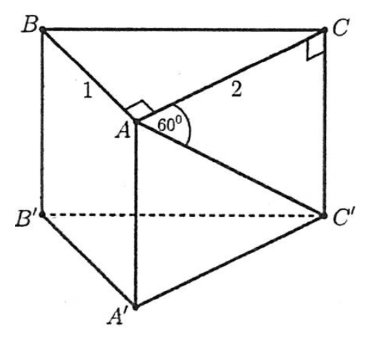
Vî \(A B C .A^{\prime} B^{\prime} C^{\prime}\) là lăng trụ đứng nên \(A A^{\prime} \perp(A B C) \Rightarrow A A^{\prime} \perp A B\)

Mà \(A C \perp A B~~~~~~(1)\)

Suy ra \(A B \perp\left(A C C^{\prime} A^{\prime}\right) \Rightarrow A C^{\prime} \perp A B~~~~~~~~(2)\).

Từ (1) và (2) suy ra \(C A C\) là góc phẳng nhị diện \([C, A B, C]\) và \(C A C=60^{\circ}\). 

Tam giác \(A C C^{\prime}\) vuông tại \(C\) có: 

\(\tan C^{\prime} A C=\frac{C C^{\prime}}{A C} \Rightarrow C C^{\prime}=2 \sqrt{3}\).

Thể tích khối lăng trụ đã cho là: \(V_{A B C. A^{\prime} B^{\prime} C^{\prime}}=A^{\prime} A .S_{\triangle A B C}=2 \sqrt{3}. \frac{1}{2}.1 . 2=2 \sqrt{3}\) (đơn vị thể tích).

Dễ thấy \(C C^{\prime} \perp(A B C)\) và \(C C^{\prime}=\left(A C C^{\prime}\right) \cap\left(B^{\prime} C C^{\prime}\right)\) nên \(A C B\) là góc phẳng nhị diện \(\left[A, C C^{\prime}, B^{\prime}\right]\).

Tam giác \(A B C\) vuông tại \(A\) có: \(\tan A C B=\frac{A B}{A C}=\frac{1}{2} \Rightarrow A C B \approx 26,57^{\circ}\).