Cho hình thang \(A B C D\) vuông tại \(A, B\) với \(A B=B C=\frac{A D}{2}=a\). Quay hình thang và miền trong của nó quanh đường thẳng chứa cạnh \(B C\). Tính thể tích khối tròn xoay được tạo thành.
A.
\(\pi a^{3}\)
B.
\(\frac{4 \pi a^{3}}{3}\)
C.
\(\frac{7 \pi a^{3}}{3}\)
D.
\(\frac{5 \pi a^{3}}{3}\)
Giải thích:
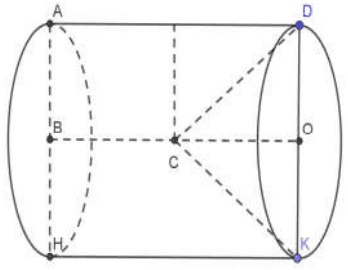
Thể tích khối tròn xoay tạo thành bằng thể tích khối trụ có hai đáy là hai đường tròn đường kính \(A H, D K\) trừ đi thể tích khối nón đỉnh \(C\) có đáy là đường tròn đường kính \(D K\).
Thể tích khối trụ bằng \(A D \cdot \pi A B^{2}=2 a \cdot \pi a^{2}=2 \pi a^{3}\).
Thể tích khối nón bằng \(\frac{1}{3} C O \cdot \pi O D^{2}=\frac{\pi a^{3}}{3}\).
Suy ra thể tích khối tròn xoay cần tìm bằng \(2 \pi a^{3}-\frac{\pi a^{3}}{3}=\frac{5 \pi a^{3}}{3}\).
Câu hỏi này nằm trong: