Thay \(x=0 ; y=3\) vào đồ thị \((P)\) thì không thỏa mãn.

Bảng biến thiên của hàm số bậc hai:

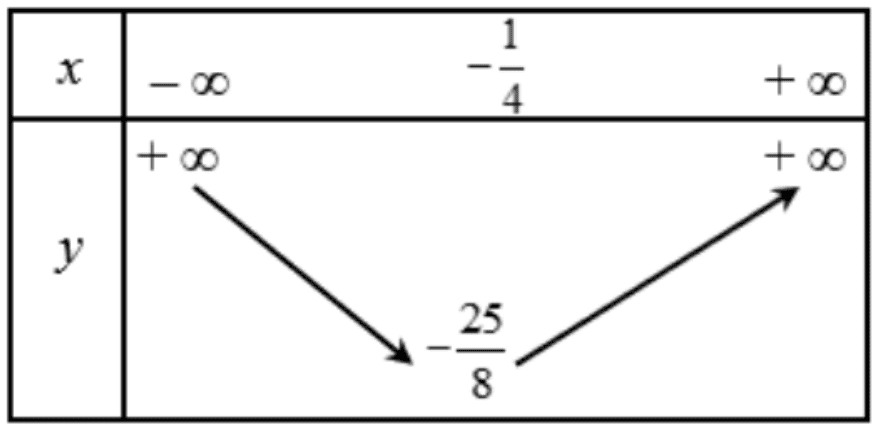
Vậy tọa độ đỉnh của hàm số bậc hai là \(I\left(-\frac{1}{4} ;-\frac{25}{8}\right)\)

Xét phương trình hoành độ giao điểm của \((P)\) và \(d: 2 x^{2}+x-3=-(m+1) x-m-2\)

\(\left.\Leftrightarrow 2 x^{2}+x-3+(m+1) x+m+2=0 \Leftrightarrow 2 x^{2}+(m+2) x+m-1=0 \quad({ }^{*}\right)\)

Để phương trình \(\left({ }^{*}\right)\) có hai nghiệm phân biệt nằm về cùng một phía đối với trục tung thì ta có điều kiện \(\left\{\begin{array}{l}\Delta\gt 0 \\ P>0\end{array} \Leftrightarrow\left\{\begin{array}{l}m^{2}-4 m+12>0 \\ \frac{m-1}{2}>0\end{array} \Leftrightarrow m>1\right.\right.\)

Vậy có 7 giá trị nguyên dương \(m \in[-3 ; 10)\) để đường thẳng \((d)\) cắt đồ thị \((P)\) tại hai điểm phân biệt nằm về cùng một phía đối với trục tung.

d) Sai: Có 7 giá trị nguyên dương \(m \in[-3 ; 10)\) để đường thẳng \((\mathrm{d})\) cắt đồ thị \((P)\) tại hai điểm phân biệt nằm về cùng một phía đối với trục tung.