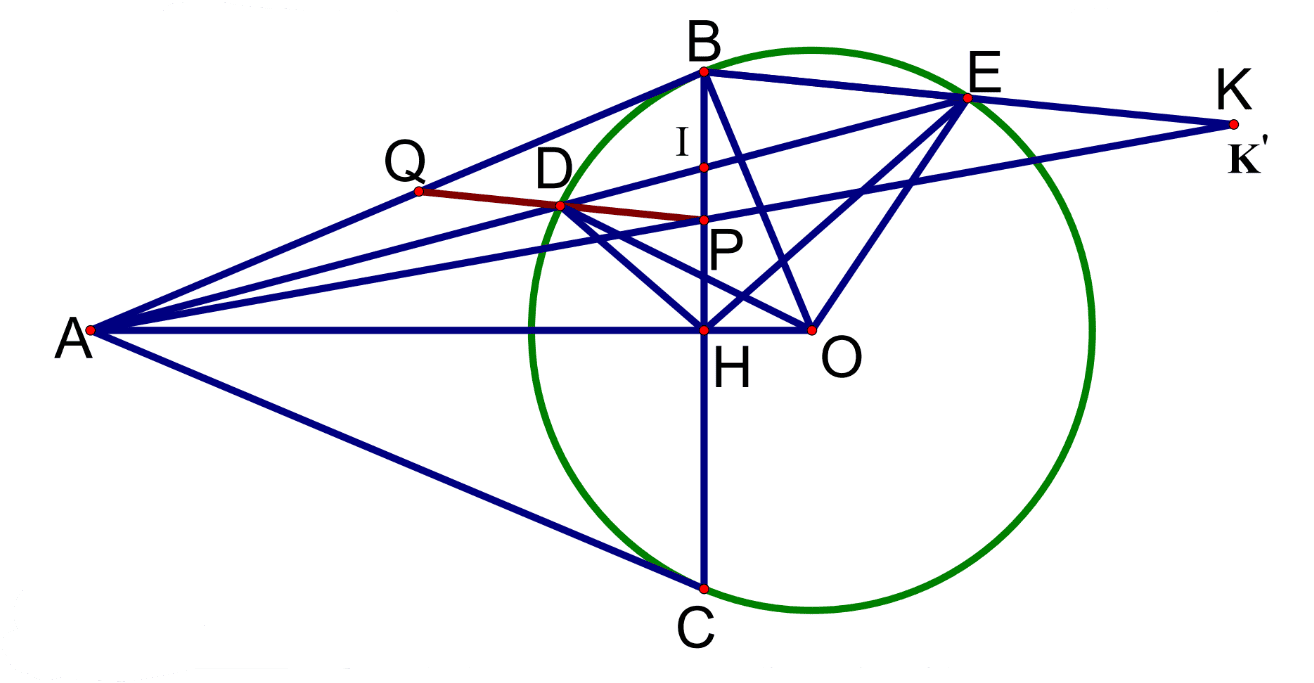
Ta có: \(\mathrm{AB}=\mathrm{AC}(\mathrm{AB}, \mathrm{AC}\) là hai tiếp tuyến của \((\mathrm{O})), \mathrm{OB}=\mathrm{OC}\) (bán kính)

Nên \(\mathrm{OA}\) là trung trực của \(\mathrm{BC}\)

Xét \(\triangle \mathrm{ABO}: \widehat{A B O}=90^{\circ}\) (AB là tiếp tuyến của \(\left.(\mathrm{O})\right), \mathrm{BH} \perp \mathrm{OA}(\mathrm{OA}\) là trung trực của \(\mathrm{BC}\) ) \(\Rightarrow A B^{2}=A H . A O \quad(a)\)

Xét \(\triangle \mathrm{ABD}\) và \(\triangle \mathrm{AEB}\) : \(\widehat{A B D}=\widehat{A E D}=\frac{1}{2} s d \widehat{B D}\) (góc nội tiếp, góc tạo bởi tia tiếp tuyến và dây)

\(\widehat{B A D}\) (góc chung). Vậy \(\triangle \mathrm{ABD} \sim \triangle \mathrm{AEB}\) (g.g) \(\Rightarrow \frac{A B}{A E}=\frac{A D}{A B} \Rightarrow A B^{2}=A D \cdot A E(b)\)

Từ (a) và (b) suy ra \(\Rightarrow A H \cdot A O=A D \cdot A E \Rightarrow \frac{A H}{A D}=\frac{A E}{A O}\)

Xét \(\triangle \mathrm{AHD}\) và \(\triangle \mathrm{AEO}: \frac{A H}{A D}=\frac{A E}{A O}(\mathrm{cmt}), \widehat{H A D}(\) chung \()\). Vậy \(\triangle \mathrm{AHD} \sim \triangle \mathrm{AEO}\) (c.g.c)

\(\Rightarrow \widehat{A H D}=\widehat{A E O}\). Do đó tứ giác \(\mathrm{OEDH}\) là tứ giác nội tiếp (đpcm)