Cho hàm số \(y=f(x)\) có đạo hàm trên \(\mathrm{R}\) và có đồ thị \(y=f^{\prime}(x)\) như hình vẽ.
Xét hàm số \(g(x)=f\left(x^{2}-2\right)\).
Mệnh đề nào sau đây sai?
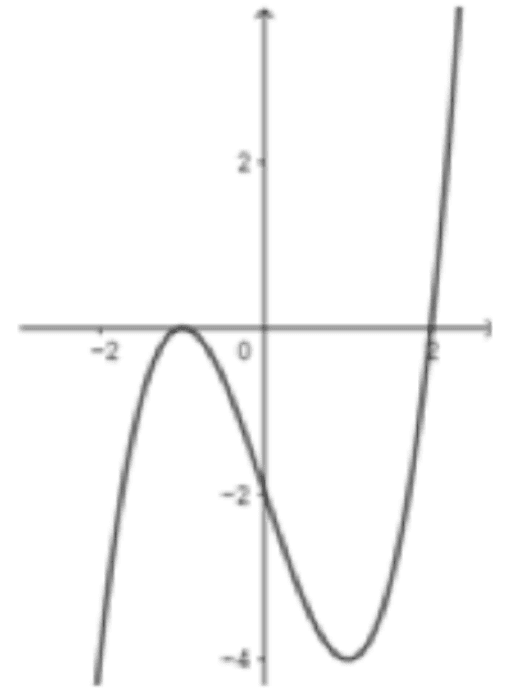
A.
Hàm số \(g(x)\) nghịch biến trên \((0 ; 2)\).
B.
Hàm số \(g(x)\) đồng biến trên \((2 ;+\infty)\).
C.
Hàm số \(g(x)\) nghịch biến trên \((-\infty ;-2)\).
D.
Hàm số \(g(x)\) nghịch biến trên \((-1 ; 0)\).
Giải thích:
\(\begin{array}{l}\text { Ta có } g(x)=f\left(x^{2}-2\right) \\ g^{\prime}(x)=f^{\prime}\left(x^{2}-2\right) \cdot 2 x \\\end{array}\)
\(g^{\prime}(x)=0 \Leftrightarrow\left[\begin{array}{l}x=0 \\ f^{\prime}\left(x^{2}-2\right)=0\end{array} \Leftrightarrow\left[\begin{array}{l}x=0 \\ x^{2}-2=-1 \\ x^{2}-2=2\end{array} \Leftrightarrow\left[\begin{array}{l}x=0 \\ x=1 \\ x=-1 \\ x=2 \\ x=-2\end{array}\right.\right.\right.\)
Ta có \(g^{\prime}(3)=6 \cdot f^{\prime}(7)\gt 0, g^{\prime}(x)\) đổi dấu qua các nghiệm đơn hoặc bội lẻ, không đổi dấu qua các nghiệm bội chẵn nên ta có bảng xét dấu \(\mathrm{g}^{\prime}(\mathrm{x})\) :

Câu hỏi này nằm trong: