Cho hình tam giác đều \(S . A B C\) có cạnh đáy bằng \(a\) và cạnh bên bằng \(b(a \neq b)\). Các mệnh đề sau đúng hay sai?
a) Đoạn thẳng \(M N\) là đường vuông góc chung của \(A B\) và \(S C\) ( \(M\) và \(N\) lần lượt là trung điểm của \(A B\) và \(S C\)).
A.
True
B.
False
Giải thích:
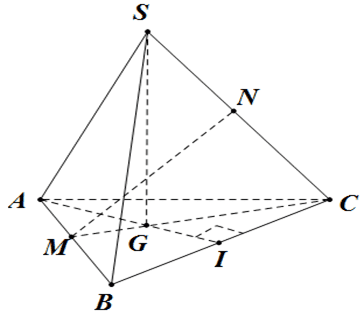
\(\ \triangle S A G=\triangle S B G=\triangle S C G\). Suy ra góc giữa các cạnh bên và đáy bằng nhau.
\(\left\{\begin{array}{l}S A=S B=S C \\ A B=A C=B C\end{array}\right.\), suy ra hình chiếu vuông góc của \(S\) lên trên mặt phẳng \((A B C)\) là trọng tâm tam giác \(A B C\).
\(B C \perp(S A I) \Rightarrow B C \perp S A\)
Câu hỏi này nằm trong: