Điều kiện: \(y \neq-4 ; x \in(-1 ; 5)\)

\(\begin{array}{l}\log _{\sqrt{3}}\left(y^{2}+8 y+16\right)+\log _{2}[(5-x)(1+x)]=2 \log _{3} \frac{5+4 x-x^{2}}{3}+\log _{2}(2 y+8)^{2} \\\Leftrightarrow \log _{\sqrt{3}}(y+4)^{2}+\log _{2}[(5-x)(1+x)]=2 \log _{3} \frac{(5-x)(1+x)}{3}+\log _{2} 4 \cdot(y+4)^{2} \\\Leftrightarrow 2 \log _{3}(y+4)^{2}-\log _{2}(y+4)^{2}=2 \log _{3}[(5-x)(1+x)]-\log _{2}[(5-x)(1+x)]\end{array}\)

Xét hàm số \(f(t)=2 \log _{3} t-\log _{2} t, \forall t \in(0 ;+\infty)\)

\(\begin{array}{l}\Rightarrow f^{\prime}(t)=\frac{2}{\mathrm{t} \cdot \ln 3}-\frac{1}{\mathrm{t} \cdot \ln 2}=\frac{1}{\mathrm{t}}\left(\frac{2}{\ln 3}-\frac{1}{\ln 2}\right)\gt 0, \forall t \in(0 ;+\infty) \\ \Rightarrow f\left((y+4)^{2}\right)=f((5-x)(1+x)) \Leftrightarrow(y+4)^{2}=5+4 x-x^{2} \Leftrightarrow(y+4)^{2}+(x-2)^{2}=9(1) \end{array}\)

\(\Rightarrow M(x ; y) \in(C)\) tâm \(I(-4 ; 2), R=3\) và \( O M=\sqrt{x^{2}+y^{2}}\)

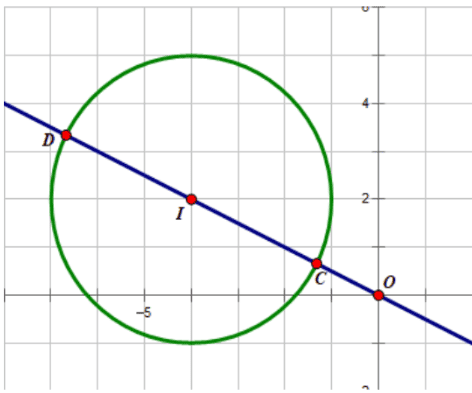
Ta có \(O M_{\min }=O I-R, O M_{\max }=O I+R\)

\(\begin{array}{l}2 \sqrt{5}-3-m \leq \sqrt{x^{2}+y^{2}}-m \leq 2 \sqrt{5}+3-m(2) \\P \leq 10 \Rightarrow\left\{\begin{array}{l}2 \sqrt{5}+3-m \leq 10 \\2 \sqrt{5}-3-m \geq-10\end{array} \Leftrightarrow 2 \sqrt{5}-7 \leq m \leq 2 \sqrt{5}+7\right.\end{array}\)

Vậy \(S=\{-2 ;-1 ; 0 \ldots ; 10 ; 11\}\) có 14 số nguyên.

Số tập con khác rỗng của \(S\) là \(2^{14}-1=16383\)