Giả sử \(A, B\) là hai điểm phân biệt trên đồ thị của hàm số \(y=\log _{3}(5 x-3)\) sao cho \(A\) là trung điểm của đoạn \(O B\).
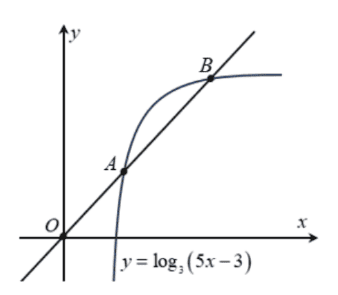
a) Hoành độ của điểm \(B\) là một số nguyên.
A.
B.
Giải thích:
Gọi \(A\left(x_{1}, \log _{3}\left(5 x_{1}-3\right)\right)\).
Vì \(A\) là trung điểm \(O B\) nên \(B\left(2 x_{1} ; 2 \log _{3}\left(5 x_{1}-3\right)\right)\).
Vì \(B\) thuộc đồ thị của hàm số \(y=\log _{3}(5 x-3)\) nên
\(2 \log _{3}\left(5 x_{1}-3\right)=\log _{3}\left(10 x_{1}-3\right) \Leftrightarrow\left\{\begin{array}{l}5 x_{1}-3\gt 0 \\ 10 x_{1}-3>0 \\ \left(5 x_{1}-3\right)^{2}=10 x_{1}-3\end{array}\right.\)
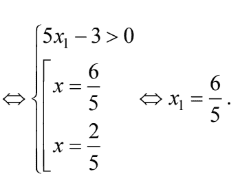
Vì thế \(A\left(\frac{6}{5} ; 1\right), B\left(\frac{12}{5} ; 2\right) \Rightarrow A B=\frac{\sqrt{61}}{5}\).
Hình chiếu điểm \(B\) xuống trục hoành là \(H\left(\frac{12}{5} ; 0\right) \Rightarrow B H=2\) và \(O H=\frac{12}{5} \Rightarrow S_{\triangle O B H}=\frac{12}{5}\)
Câu hỏi này nằm trong: