Cho tam giác \(A B C\) vuông cân tại điềm \(A\) và \(B C=a\). Trên đường thă̆ng qua \(A\) vuông góc với mặt phẳng \((A B C)\) lấy điểm \(S\) sao cho \(S A=\frac{a \sqrt{6}}{2}\). Tính số đo góc giữa đường thẳng \(S B\) và \((A B C)\).
A.
\(30^{\circ}\)
B.
\(45^{\circ}\)
C.
\(60^{\circ}\)
D.
\(75^{\circ}\)
Giải thích:
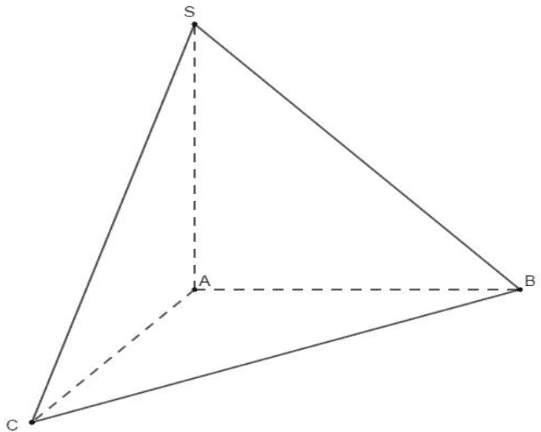
Do \(S A \perp(A B C) \Rightarrow \overline{(S B,(A B C)})=\widehat{S B A}\).
Tam giác \(A B C\) vuông cân tại điểm \(A\) nên ta có \(2 A B^{2}=B C^{2} \Rightarrow A B=\frac{a}{\sqrt{2}}\).
Trong tam giác vuông \(S A B\), ta có \(\tan \widehat{S B A}=\frac{S A}{A B}=\frac{\frac{a \sqrt{6}}{2}}{\frac{a}{\sqrt{2}}}=\sqrt{3} \Rightarrow \text{cung } S B A=60^{\circ}\).
Câu hỏi này nằm trong: