Cho ba số thực dương \(a, b, c\) khác 1. Đồ thị các hàm số \(y=a^{x}, y=b^{x}, y=c^{x}\) được cho trong hình vẽ dưới đây. Mệnh đề nào dưới đây đúng?
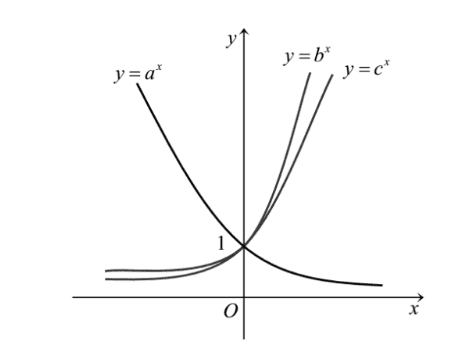
a) Hai hàm số \(y=a^{x}\) và \(y=c^{x}\) nghịch biến trên \(\mathbb{R}\).
A.
True
B.
False
Giải thích:
Ta có: Hàm số \(y=a^{x}\) nghịch biến trên \(\mathbb{R} \Rightarrow 0\lt a\lt 1\).
Các hàm số \(y=b^{x}\) và \(y=c^{x}\) đồng biến trên \(\mathbb{R}\) nên \(b, c\gt 1\).
Ta lại có \(\forall x>0\) thì \(b^{x}>c^{x} \Rightarrow b>c\).
Vậy \(a\lt c\lt b\).
Câu hỏi này nằm trong: