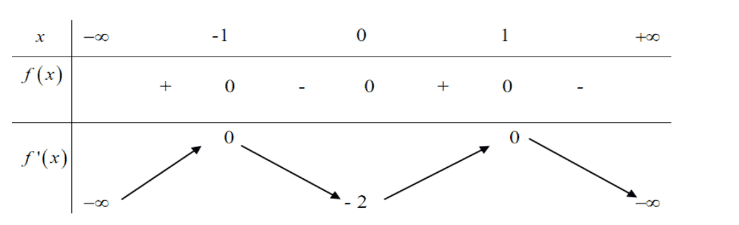
Cho hàm số \(f(x)\) có bảng biến thiên như sau:
Số nghiĉ̣m thuộc đoạn \(\left[-\pi ; \frac{5 \pi}{2}\right]\) của phương trình \(f(\sin x)=-1\)
A.
7
B.
8
C.
5
D.
6
Giải thích:
Đặt \(t=\sin x\).
Khi đó \(t^{\prime}=\cos x\)\(t^{\prime}=0 \Leftrightarrow x=\frac{\pi}{2}+k \pi, k \in \mathbb{Z}\).
Vì \(x \in\left[-\pi ; \frac{5 \pi}{2}\right]\) nên \(x \in\left\{-\frac{\pi}{2} ; \frac{\pi}{2} ; \frac{3 \pi}{2} ; \frac{5 \pi}{2}\right\}\)
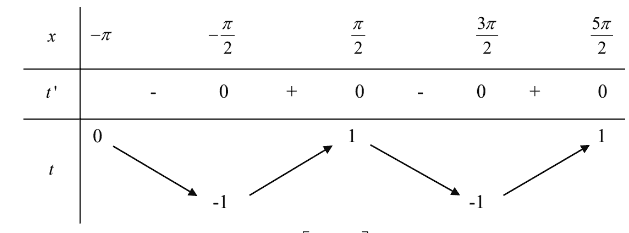
Dựa vào bảng biến thiên ta có \(x \in\left[-\pi ; \frac{5 \pi}{2}\right]\) nên \(t \in[-1 ; 1]\); ứng với mỗi \(t \in(-1 ; 0)\) cho ta 4 nghiệm \(x\); úng với mỗi \(t \in(0 ; 1)\) cho ta 3 nghiệm \(x\).
Phương trình \(f(\sin x)=-1\) trở thành \(f(t)=-1, \forall t \in[-1 ; 1]\).
Đây là phương trình hoành độ giao điểm của hàm số \(y=f(t)\) và đường thẳng \(y=-1\).
Dựa vào bảng biến thiên đề bài cho, ta có \(f(t)=-1 \Leftrightarrow\left[\begin{array}{l}t=a \in(-1 ; 0) \\ t=b \in(0 ; 1)\end{array} \quad\left({ }^{* *}\right)\right.\)
Từ (*) và (**) ta suy ra có 7 nghiệm \(x\) thóa mãn.
Câu hỏi này nằm trong: